Ausgewählte, in der Analysis untersuchte Kurven

Mit der einfachen Sinuslinie



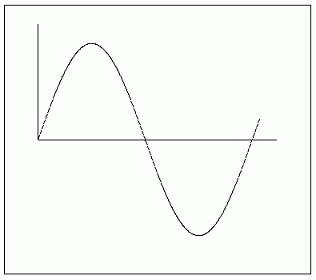
kann man, wenn sie verzerrt, verschoben, gedreht und mit anderen kombiniert wird, eine Menge machen, zum Beispiel ein farbiges Band erzeugen



oder, wie bereits an anderer Stelle gezeigt, ein Stück "Gardine" (Store):



Bewegt sich ein Punkt der x,y-Ebene in Abhängigkeit von der Zeit sinusförmig in beiden Achsenrichtungen hin und her, entstehen Lissajous-Kurven unterschiedlichsten Aussehens, von denen zwei hier wiedergegeben seien:

 
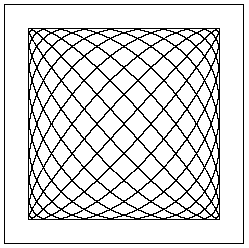
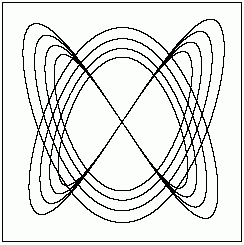
(Bei der zweiten Kurve wird der Punkt in seiner Bewegung ständig etwas abgebremst.)

Ebenfalls mit der Sinusfunktion und ihrem Pendant, der Kosinusfunktion, (sowie einigem anderen) erhält man die folgenden beiden Kurven:

 

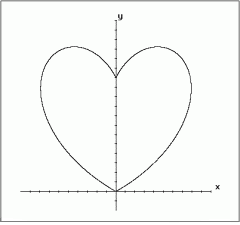
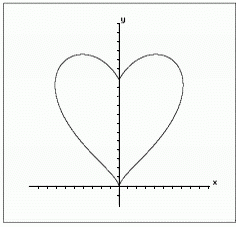
Mathematisch wird die linke durch das Gleichungspaar x = a (-φ² + 40φ + 1200) sin(πφ/180), y = a (-φ² + 40φ + 1200) cos(πφ/180) beschrieben. Dabei bedeutet φ (im Bereich von 0 bis 60 Grad) den Winkel, den die Verbindungsstrecke zwischen einem Punkt auf der Herzlinie und dem Koordinatenursprung mit der positiven y-Achse bildet. a ist ein geeignet zu wählender Maßstabsfaktor, z. B. 1/100. Die konkave Spitze bei der rechten Figur wird durch einen kleinen Zusatz erreicht.

Weniger "romantisch" als die Herzkurven und eher unscheinbar wirkt die folgende Figur



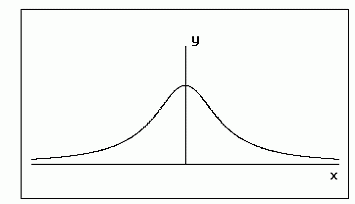
mit der einfachen Gleichung y=1/(1+x²), doch besitzt sie eine Besonderheit: obwohl sich die Kurve nach beiden Seiten bis ins Unendliche erstreckt und dabei nie die x-Achse berührt, so daß ein immer feiner werdender Spalt übrig bleibt, hat der Inhalt der Fläche zwischen ihr und der x-Achse trotzdem einen endlichen (Grenz)wert. Seine Größe ist bekannt und gleich der Kreiszahl Pi.

Die Kurve heißt "Versiera" und ist mit dem Namen von Maria Agnesi verbunden, einer berühmten italienischen Mathematikerin des 18. Jahrhunderts, die in ganz Europa geschätzt und bewundert wurde. Auf der Höhe ihrer Karriere wandte sie sich von der Wissenschaft ab und widmete sich fortan nur noch der Pflege alter und kranker Menschen, als deren "Engel" sie von vielen bezeichnet wurde. Über Maria Agnesi findet man eine Reihe interessanter Beiträge im Internet, z. B. hier. (Anm.: bei "siebensprachiges Wunder" müsste es "miracolo" statt "oracolo" heißen.)

Eine große Vielfalt von Kurven entsteht, wenn ein Kreis im Innern eines anderen Kreises oder außen auf ihm abrollt (Hypo- bzw. Epizykloiden). Auch hierzu eine geringe Auswahl:

  

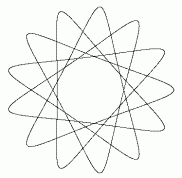
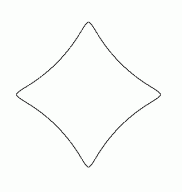
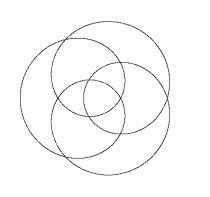
Die dafür gültigen, Sinus und Kosinus enthaltenden Formeln wiederzugeben und zu erklären, würde hier zu weit führen. Experimentell kann man die Kurven mit dem als Kinderpielzeug bekannten "Spirographen" gewinnen.


Ohne die beiden genannten Funktionen erhält man ein Kleeblatt und ein Ei:

 

*

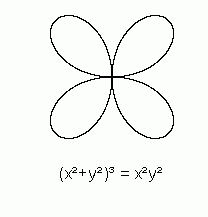
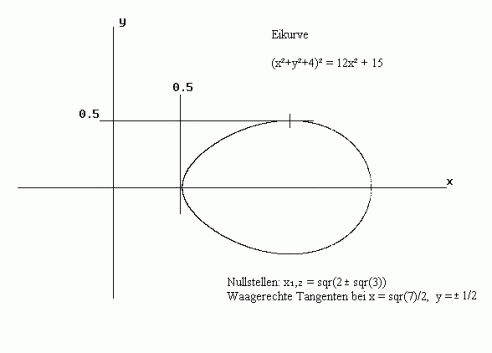
Bei der komplexen Abbildung w=1/z (z=x+iy, w=u+iv) entspricht einem Kreis der z-Ebene, der nicht durch den Ursprung geht, ein Kreis in der w-Ebene, der dort ebenfalls den Ursprung meidet. Man nennt die beiden Kreise miteinander "verwandt" und spricht von Kreisverwandtschaft. Bewegt sich statt dessen der Originalpunkt auf einer Hyperbel mit der Gleichung y=a/x, a>0, dann ist die Bildkurve eine Lemniskate mit a(u²+v²)²=-uv. Beide Kurven sind also über die Abbildung w=1/z ebenso miteinander verwandt wie die genannten Kreise. - Wählt man als Bahnkurve des Originalpunktes die Parabel mit der Gleichung y=x²/3-3/4, erhält man eine Kardiode, deren Gleichung 9(u²+v²)²+(u²+v²)v+4u²=0 lautet. Auch hier besteht durch w=1/z eine Kurvenverwandtschaft. Die beiden folgenden Figuren veranschaulichen dies (Originalkurve schwarz, Bildkurve blau):

 

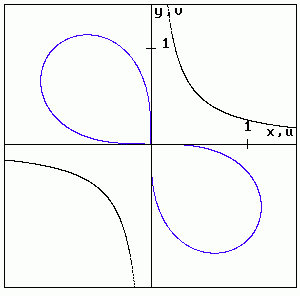
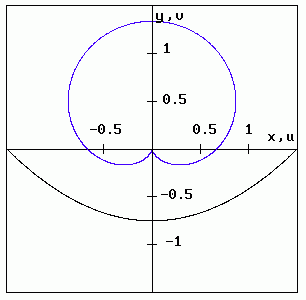
(Kardioide bedeutet übrigens auf deutsch Herzkurve. Sie ähnelt, vor allem, wenn man sie umdreht, unserem "Lebensmotor" mehr als die spitze Form, in der das Herz gewöhnlich symbolisiert wird. Entdeckt/erfunden und auf ihre Eigenschaften sorgfältig untersucht wurde die Kardioide schon im 17. Jahrhundert. Offensichtlich stellte man sich damals das Herz als einen rundlichen Beutel vor, der es im wesentlichen ja auch ist. Wann und warum die Spitze hinzukam, wäre interessant zu erfahren.)^{1) 2)}    Herzkurven

Eng mit den komplexen Zahlen hängen auch bestimmte Fraktale zusammen, unter ihnen das berühmte "Apfelmännchen", das hier in perspektivischer Lage und in direkter Aufsicht gezeigt wird:

 

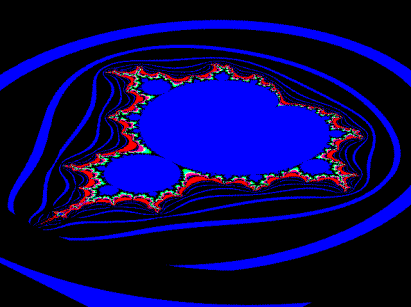
Sein warzenartig zerklüfteter Hauptteil wird von einer Kardioide begrenzt und durchsetzt (click).

Die oben erwähnte Lemniskate, eine schräg liegende Acht, welche oft auch in anderer Position gezeichnet wird, ziert eine norwegische Münze. Wie es dazu kam, erfährt man hier: http://www.w-volk.de/museum/coins.htm (Wolfgang Volk: Zeugnisse über Mathematiker, Eine virtuelle Ausstellung).

Lese-Empfehlung: Jutta Gut - "Spitzen, Schlingen, Ostereier - Kurven dritten Grades"
http://members.chello.at/gut.jutta.gerhard/kurven3_1.htm

--------------------------------------------------------------------------
¹⁾ Einige Jahre, nachdem ich das Obige schrieb, entdeckte ich im Athener Kerameikos-Museum dies:

Die dort gezeigten, unter ungünstigen Bedingungen aufgenommenen, herzförmigen Objekte, deren Verwendungszweck mir unbekannt blieb, sind mehrere tausend Jahre alt. Die auf einigen von ihnen erkennbare Kurve erinnert in ihrem unteren Teil an eine Kardioide.

Aus jener Zeit stammen auch diese Keramikscheiben in demselben Museum:

Sie zeigen Spiralen, eine weitere interessante Kurvenart, auf die hier jedoch nicht näher eingegangen werden soll.

Anmerkung: auf der linken Scheibe ergeben die Spiralbögen ein ziemlich regelmäßiges Siebeneck. Die Zahl 7 spielte im Altertum eine große Rolle, vgl. [1]. Unter anderem glaubte man, daß die Erde von sieben "Wandelsternen" umkreist wird: Sonne, Mond, Merkur, Venus, Mars, Jupiter und Saturn - das sind mit bloßem Auge erkennbare Himmelskörper unterschiedlicher Größe und Helligkeit, die sich vor dem Hintergrund der Fixsterne bewegen, vgl. [2]. Es mag sein, daß die linke Spiralfigur ein künstlerischer Ausdruck für diese Vorstellung ist. Dann würde der Kreis in der Scheibenmitte der Erde entsprechen. Da diese, anders als die Sonne, selber keine Strahlen aussendet, kann man sich fragen, was der in dem Kreis enthaltene Stern bedeuten soll. Vielleicht ist er rein dekorativ. Mit seinen sieben Zacken könnte er aber auch ein religiöses Symbol sein, weil in verschiedenen alten Kulturen den sieben Wandelsternen Götter zugeordnet wurden. - Übrigens bilden auf der rechten Keramikscheibe die Spiralen ein (unregelmäßiges) Achteck.
[1] Sieben, Wikipedia   [2] Blinde Kuh - Unser Sonnensystem, farbige Kreisfigur im Abschnitt über Claudius Ptolemäus

An der Maserung hölzerner Stuhllehnen:

fand ich noch zwei Scharen ellipsen- bzw. hyperbelähnlicher Kurven.

²⁾ Martin Luther (1483 bis 1546) zeichnete in der nach ihm benannten "Lutherrose" das Herz noch ohne Spitze, vgl. hier.

Zurück zu Geometrische Figuren
Zurück zur Hauptseite