Das Zerschneiden einer geometrischen Figur und das Zusammensetzen der Teile zu einer neuen mit dem Ziel, eine Aufgabe zu lösen oder etwas zu beweisen, hat eine lange Tradition. Ein einfaches Beispiel hierfür ist dieser bekannte Beweis des Satzes von Pythagoras (einer von über hundert!) ganz ohne Rechnung:
In [1] und [2] wird dieses von dem syrischen Mathematiker Thabit ibn Qurra (836-901) erdachte Problem genannt:
Wie groß ist die Fläche des das Dreieck umschließenden Rahmens im Vergleich zur Fläche des Kreises?
Ebenfalls ohne zu rechnen ging ich so vor:
Erklärung: der obere Teil der Originalfigur wird in Einzelstücken schrittweise in die untere Kreishälfte übertragen. Dort, wo ein Stück weggenommen wurde, bleibt eine leere, weiße Fläche zurück, und dort, wo es hingebracht wurde, sieht es, wie oben, dunkelorange aus. Zum Schluss ist die gesamte obere Hälfte unten angekommen und füllt zusammen mit dem, was schon da war, die untere Kreisflächenhälfte ganz aus. Ergebnis: die Fläche des Rahmens ist halb so groß wie die Kreisfläche. Das zeigt auch die Rechnung, auf die ich hier verzichte.
Anmerkung: Der Unterschied benachbarter Teilfiguren fällt manchmal kaum auf, so dass man sehr genau hinschauen muss, um ihn zu bemerken. Eventuell lässt sich das hier angestrebte Ziel durch eine andere Art des Zerlegens und Zusammensetzens schneller erreichen.
"Beweis ohne Worte"
Unter dieser Überschrift steht auf dem Matheplaneten hier eine Aufgabe, die nicht ganz klar formuliert ist
und ergebnislos blieb. Im Kern lautet sie unter Verwendung der folgenden Figur:
Ohne Worte (und Rechnung) ist zu zeigen, dass die Fläche des inneren Quadrats ein Fünftel der Fläche
des äußeren beträgt.
Eine Lösungsmöglichkeit ist diese:
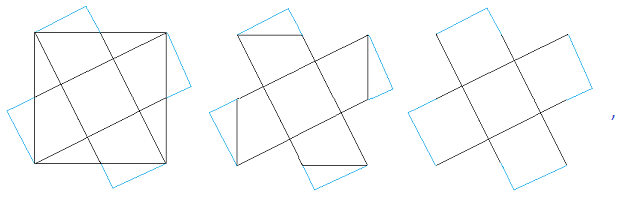
oder man verschiebt die kleinen Dreiecke der Ausgangsfigur ohne Punktspiegelung so, dass sich dieselbe,
aus fünf gleich großen Quadraten bestehende Endfigur ergibt.
Nachtrag
Beweise ohne Worte, die rein auf Anschauung beruhen, sind beliebt, weil sie schneller und weniger umständlich sein können als rechnerische Beweise. Man kann sich dabei aber auch täuschen, wie das folgende Beispiel zeigt.
Bedeutet n die Anzahl der Punkte auf dem Kreisumfang, so liegt es nahe zu behaupten: die Anzahl der durch Diagonalen und Kreisbogenstücke begrenzten Kreisflächenteile beträgt allgemein 2n-1, wenn die Bildsequenz sinngemäß weiter fortgesetzt wird. Diese Behauptung ist falsch, denn der als nächstes vorgesehene Kreis mit regelmäßigem Sechseck besteht nicht aus 32 Teilen, die sich für n=6 ergeben würden. Wie viele es tatsächlich sind, zeigt eine rasch gezeichnete Handskizze. Mehr zu alledem s. hier.
-------------------------
[1] https://www.spektrum.de/fm/976/1193946.pdf
[2] https://www.spektrum.de/raetsel/dreieck-sechseck-und-kreis/1660352
Zurück zur Themenübersicht, Teil 2