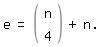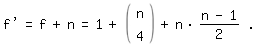Induktives Vorgehen beim Auffinden von Gesetzmäßigkeiten ist in der Physik wie in der Mathematik verbreitet und führt oftmals, aber nicht immer, zu brauchbaren Ergebnissen. Ein Beispiel, bei dem es funktioniert, ist die Addition der Kuben aufeinander folgender natürlicher Zahlen. Dabei ergibt sich:
13=12, 13+23=32, 13+23+33=62, 13+23+33+43=102,
und die Vermutung liegt nahe, daß für jedes natürliche n gilt:
13+23+33+...+n3=dn2, wobei dn=1+2+3+...+n
die n-te der Zahlen 1,3,6,10,... ist, die, weil man sie so
veranschaulichen kann, Dreieckszahlen heißen.
Gesetzmäßigkeiten, die durch ein paar Anfangsbeispiele, d. h. unvollständig induktiv, gefunden wurden, müssen anschließend mit Hilfe der vollständigen Induktion oder auf anderem Wege allgemein bewiesen werden. Wird darauf verzichtet, gerät man unter Umständen in eine böse Falle.
Bei den Dreieckszahlen fand nach einer oft zitierten Anekdote der erst neunjährige Gauß heraus, daß sie sich für jedes natürliche n mit dem Term n(n+1)/2 viel leichter als durch stures Aufsummieren berechnen lassen. Dabei wendete er ein eigenes, nicht-induktives Verfahren an, das seinem Lehrer unbekannt war und ihn sehr beeindruckte.
Liegt ein auf analytischen oder konstruktiven Überlegungen beruhendes Beweisverfahren nicht auf der Hand und findet man auch bei angestrengtem Nachdenken nichts dergleichen, bleibt einem kaum anderes übrig, als den induktiven Weg zu versuchen. Dies soll bei der folgenden geometrischen Aufgabe geschehen:
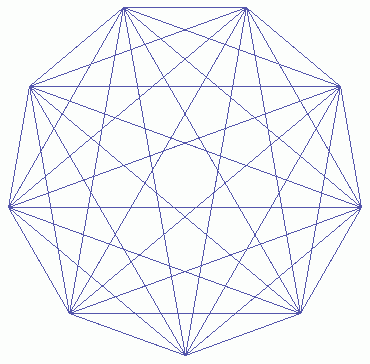
In wieviele Teile wird die Fläche eines Kreises durch die Diagonalen eines auf dem Kreisumfang liegenden, regelmäßigen n-Ecks zerlegt?
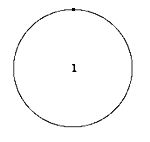
Um für den Anfang möglichst viel Zahlenmaterial zu haben, betrachten wir dabei auch das "Eineck" und "Zweieck":
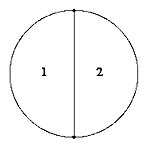
xxxxx
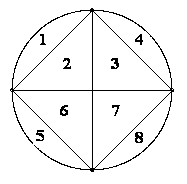
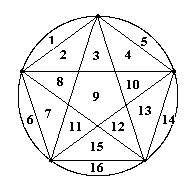
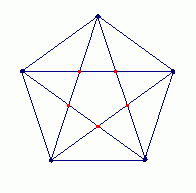
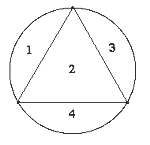
Bei diesen fünf Figuren ist die Antwort einfach: bedeutet n die Anzahl der Ecken, dann wird der Kreis in 2n-1 Bereiche zerlegt.
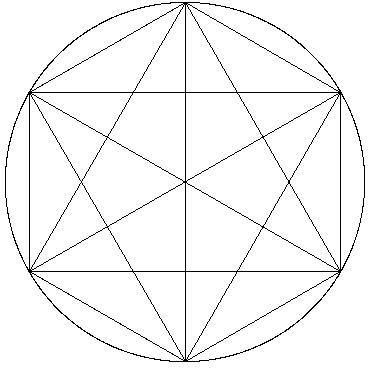
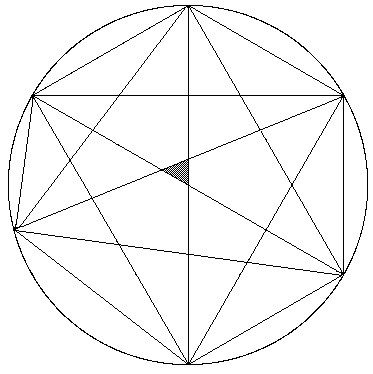
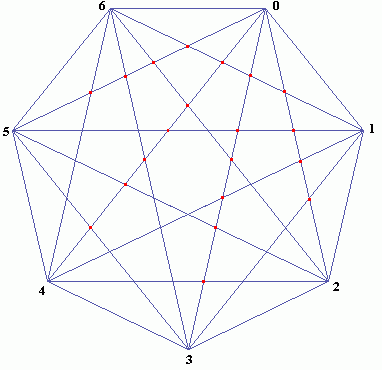
Doch Vorsicht! Beim nächsten Schritt erhält man statt der erwarteten 32 Teile nur 30 (wir haben sechs Sektoren mit fünf Feldern):
xxxxxxxxxxxxxxxxxx
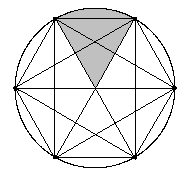
Der gefundene Term 2n-1 ist für n>5 falsch – die Induktivfalle hat zugeschnappt! Wodurch muß man ihn bei beliebigem n ersetzen,
und wie läßt sich das begründen?
Hans-Jürgen
|
Re: Induktivfalle |
|
|
|
Re:
Induktivfalle |
|
|
|
Re:
Induktivfalle |
|
|
|
Re:
Induktivfalle |
|
|
|
Re:
Induktivfalle |
|
|
|
Re:
Induktivfalle |
|
Hi,
|
)
|
Re:
Induktivfalle |
|
erhalten, weil ich nicht - wie du - an die Binomialkoeffizienten gedacht
hatte. |
------------------------------ 1) s. Anhang, nicht auf dem MP
Nachtrag (2.2.2022
): Statt n(n-1)/2 in der Gl. für f ' kann man auch schreiben "n über 2", so dass sie die schöne Form
annimmt. Diesen Hinweis verdanke ich Wally hier im Beitrag No. 12.
Wegen "n über 0" = 1 gilt auch
was man mit dem Pascalschen Dreieck veranschaulichen kann:
(mehr dazu s. a. hier)
Wie oben vermerkt, bezieht sich das Vorstehende auf regelmäßige Vielecke mit ungerader Eckenzahl (mit Ausnahme des Quadrats). Deshalb sind nur die schwarzen Zahlen hinter den blauen Zeilen Lösungen der gestellten Aufgabe. Zwar erfüllen auch die Zahlen hinter den roten Zeilen die Gl. (2); aber die Teilflächenanzahlen stimmen nicht:
Die Zahlen in Klammern sind die aus der Tabelle.
Für Vielecke mit gerader Eckenzahl gilt eine sehr viel kompliziertere Formel als (2), s. u.
Auf dem Matheplaneten wird hier im Beitrag 20 vorgeschlagen, den durch die Mehrfach-Diagonalenschnittpunkte entstandenen Unterschied dadurch zu beseitigen, dass weitere Teilflächen in Gedanken hinzugenommen werden.2) Die gewünschten, in Klammern stehenden Flächenanzahlen ergeben sich, wenn man je Dreifachschnittpunkt eine Fläche hinzunimmt, bei Vierfachschnittpunkten je drei, bei Fünffachschnittpunkten je sechs und je Sechsfachschnittpunkt zehn. (Leicht zu merken: 1,3,6,10 sind Dreieckszahlen.)
Damit gilt:
beim Sechseck: 30+1*1=31; beim Achteck: 88+8*1+1*3=99;
beim Zehneck: 230+2*10*1+1*6=256; beim Zwölfeck: 456+3*12*1+24*1+12*3+1*10=562.
Veranschaulicht wird das hier:
Anzahl und Art der Kreise sind von Vieleck zu Vieleck sehr uneinheitlich; eine Regel für sie wie für die darunter stehenden Differenz-Zahlen lässt sich nicht erkennen. Deshalb gebe ich es auf, weiter nach der Anzahl von Teilflächen bei beliebiger gerader Eckenzahl zu suchen.
Anmerkung: dass mein Entschluss nicht verkehrt ist, sehe ich nachträglich an dieser Riesenformel:
aus: https://www.youtube.com/watch?v=iJ8pnCO0nTY (Video)
Die Formel wird nur kurz gezeigt und nicht erklärt; die Originalarbeit findet sich hier.
-------------------------------
2) Vielleicht ist das so wie oben bei mir gemeint, wo durch Verschieben eines Punktes auf dem Umkreis eine weitere Fläche entsteht:
und das Vieleck unregelmäßig wird.
Zurück zur Themenübersicht