Potenzreihendarstellung ohne Taylor/McLaurin
Bekanntlich gilt für die Taylorreihe einer Funktion
in der McLaurinschen Form:
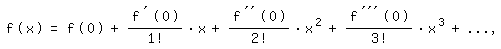
d. h., um mit ihrer Hilfe die Funktion durch eine unendliche
Potenzreihe darzustellen, muß man sie fortlaufend ableiten,
was in manchen Fällen sehr mühevoll werden kann.
Anhand einiger einfacher Beispiele soll im folgenden gezeigt
werden, wie man mit nur ein-, höchstens zweimaligem Ableiten
rasch zum Ziel kommen kann. Die betreffenden Verfahren sind
nicht neu, werden aber trotzdem nur verhältnismäßig selten
angewandt und seien deshalb hier in Erinnerung gebracht.
Beispiel 1
Es sei mit zunächst unbestimmten Koeffizienten a,b,c,...
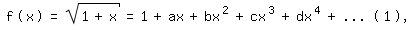
dann folgt
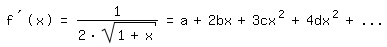
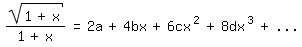
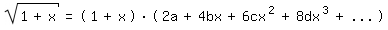

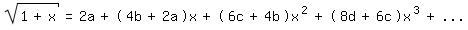
Vergleich mit (1) liefert
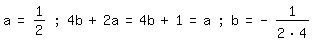
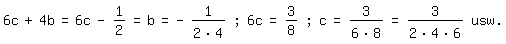
Als Ergebnis erhalten wir:
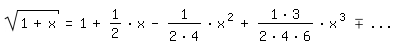
Beispiel 2
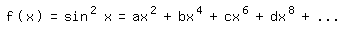
(f(x) ist gerade und f(0)=0).
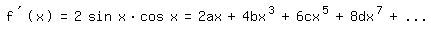
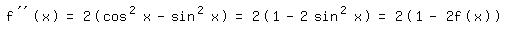
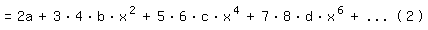
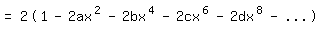
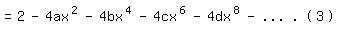
Vergleich von (2) mit (3) ergibt:
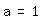
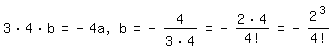
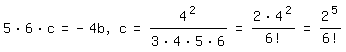
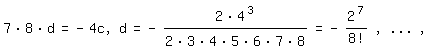
so daß gilt:
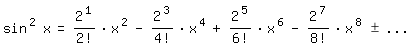
Beim Beispiel 3
brauchen wir nur einmal abzuleiten und
kommen ohne Koeffizientenvergleich aus:
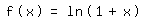
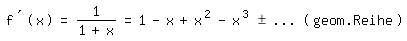
Integration ergibt:
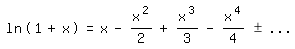
plus Integrationskonstante, die wegen ln(1)=0 gleich 0 ist.
Beispiel 4,
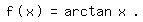
Als erstes berechnen wir die Ableitungsfunktion:
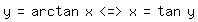
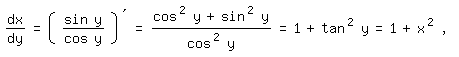
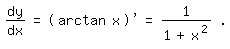
Dann wenden wir wieder die Formel für die geometrische Reihe an:
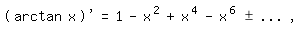
integrieren und erhalten die Reihe
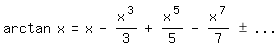
(Die Integrationskonstante ist wegen arctan 0 = 0 gleich 0.)
Beispiel 5
Sehr unbequem ist es, die Reihe für die Tangensfunktion mit Hilfe
der Taylorreihe aufzustellen. Da tan x ungerade ist, besteht die
Reihe dafür nur aus ungeraden Potenzen in x, so daß bereits der
vierte Summand die Potenz x7 enthält. Mit Taylor muß man also,
um nur vier Summanden zu erhalten, die erste bis siebte Ableitung
von tan x bilden.
Mit dem Koeffizientenvergleich geht es viel leichter. Wir setzen an:
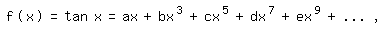
dann ist
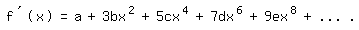
Nun gilt ganz entsprechend wie beim Arkustangens diesmal:
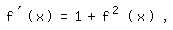
so daß sich weiter ergibt:
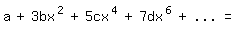
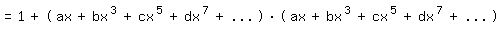
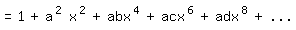
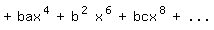
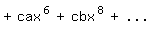
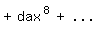
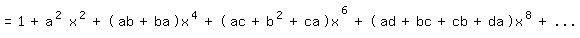
Hieraus folgt:
a=1
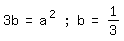
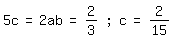
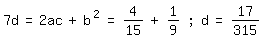
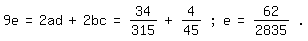
Der Anfang der Tangensreihe lautet also:
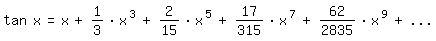
Hans-Jürgen
(27.5.04)
Zurück zur Themenübersicht