Hallo
liebe Freunde!
Es ist eine Binsenweisheit, dass in der Schule, speziell in Physik, manches
nicht oder nur zum Teil erklärt und verstanden wird, wobei die Gründe dafür
vielfältig sein können. Hierdurch sind selbst lernwillige und interessierte
Schülerinnen und Schüler öfter nicht in der Lage, ihnen gestellte Aufgaben
allein zu lösen.
Ein Beispiel dieser Art könnte die Herleitung der Umlaufzeit einer Mondfähre
sein, wie sie vor kurzem hier angefragt
wurde. Als Antwort erhielt der Fragesteller (oder die Fragestellerin?) einen
recht allgemeinen Tipp; ob er ausreichte, ist ungewiss. Es kam keine Reaktion
mehr, was entweder bedeutet, dass der oder die Betreffende zufrieden war oder
sich nicht getraute weiterzufragen.
Wie dem auch sei: im folgenden werde ich versuchen, das Problem und seine
Lösung ganz von Anfang an möglichst elementar und in kleinen Schritten zu
behandeln. Dabei wende ich mich in erster Linie an Schülerinnen und Schüler,
nicht so sehr an Studenten und Fachleute aller Art, die die darzustellenden
Grundlagen und Ergebnisse bereits kennen.
*
Wenn man einen Körper anstößt, auf den keine Kraft einwirkt, weder Reibung noch Gravitations-, elektrische oder magnetische Kräfte, bewegt er sich, ohne langsamer oder schneller zu werden, auf einer geraden Linie. Es besteht für ihn kein Anlass abzubiegen oder sein Tempo zu verändern.
Anders ist es, wenn auf den Körper eine Kraft einwirkt. Dann kann es sein, dass seine Bahn sich krümmt. Im Fall der Mondfähre ist die Gravitation die Kraft, mit der der Mond die Fähre anzieht und sie auf ihre Kreisbahn zwingt. Diese Kraft hat eine besondere Eigenschaft: sie ist stets zum Mond hin gerichtet. Genauer: die Kraft "zielt" auf den Mittelpunkt, auf das Zentrum des Mondes. Man nennt sie deshalb auch Zentralkraft. Ein anderes Wort dafür ist Zentripetalkraft; hier steckt noch das lateinische Wort "petere" mit drin, das unter anderem "aufsuchen" oder "hinstreben" bedeutet. (Diejenigen, die kein Latein hatten, sind bisweilen versucht, "Zentripedalkraft" zu sagen, doch hätte das eher mit dem Fahrrad als mit einer Raumfähre zu tun.
Die Zentripetalkraft FZ, welche die Bahn der Fähre krümmt, kann nun auf zweierlei Weise mathematisch beschrieben werden:
Zum einen gilt FZ=ΓmM/r². Hierbei bedeutet Γ ("Gamma") die universelle Gravitationskonstante, m die Masse der Fähre, M die Masse des Mondes und r den Radius der als kreisförmig angenommenen Umlaufbahn der Fähre. Die Gleichung gilt nicht nur für den Mond und die Fähre, sondern für zwei beliebige Körper mit den Massen m und M im Abstand r voneinander. Entdeckt wurde sie von Isaac Newton (1643-1727) und wird nach ihm Newtonsches Gravitationsgesetz genannt. (Anmerkung: r ist, genau genommen, der Abstand der Mittelpunkte der beiden Körper, deren Ausdehnung im Vergleich zu r als gering vorausgesetzt wird. Eine Ausnahme bilden zwei Kugeln: ihr Durchmesser kann auch größer sein.)
Nun zu der zweiten Art, einen mathematischen Term für die
Zentripetalkraft aufzustellen. Hierzu müssen wir leider sehr weit ausholen.
Wenn zum Ausdruck gebracht werden soll, dass sich die Geschwindigkeit eines
Körpers verändert, nennt man seine Bewegung beschleunigt. Im
täglichen Sprachgebrauch wird darunter meistens verstanden, dass der Körper,
etwa ein Auto, seine Geschwindigkeit vergrößert. In der Physik spricht man
dagegen auch dann von einer beschleunigten Bewegung, wenn die Geschwindigkeit
abnimmt und deutet das durch ein Minuszeichen an. Aber auch die Richtungsänderung spielt
bei der physikalischen Betrachtungs- und Sprechweise eine Rolle: selbst wenn
ein Körper wie etwa unsere Mondfähre in jeder Sekunde auf seiner gekrümmten
Bahn gleich viele Meter zurücklegt, ist seine Bewegung eine beschleunigte,
da sich ständig ihre Richtung ändert. Die vom Mond auf die Fähre
ausgeübte Zentripetalkraft bewirkt also eine Beschleunigung der
Mondfähre, auch wenn diese während ihrer Bewegung um den Mond weder schneller
noch langsamer wird. Hieran muss man sich erst einmal gewöhnen.
Warum ist das Herumreiten auf der Beschleunigung so wichtig? Weil
Beschleunigungen und Kräfte eng miteinander zusammenhängen, und auf
eine bestimmte Kraft, die Zentripetalkraft, wollen wir ja hinaus.
Wie definiert man nun Beschleunigung mathematisch?
Um das zu beantworten, wenden wir uns zunächst der einfacheren Frage zu: wie
wird "Geschwindigkeit" definiert? Die Antwort scheint trivial:
Geschwindigkeit = Weg durch (dafür benötigte) Zeit, v=s/t. Dies ist aber nur
ein Sonderfall, der darin besteht, dass die Geschwindigkeit während der
gesamten untersuchten Bewegung konstant bleibt. Nur dann kann man
eine beliebig große Messstrecke s wählen und die dafür benötigte Zeit t messen. Verändert sich
die Geschwindigkeit dagegen im Laufe der Bewegung, muss man mehrmals messen und
dabei möglichst kleine Wegabschnitte in Betracht ziehen, je kleiner desto
besser. (Dass dadurch die Messfehler bei den Teilstrecken und den gemessenen, nun
nur noch sehr kurzen Zeiten steigen und die erhaltenen einzelnen v-Werte
merklich verfälschen können, steht auf einem anderen Blatt. Hier geht es nur um
das Gedankliche.)
Weg- und Zeitabschnitte werden mit dem griechischen Δ ("Delta")
bezeichnet, das dem lateinischen D entspricht. Damit wird angedeutet, dass es
sich dabei um Differenzen handelt, etwa so: Δs=s2-s1,
wobei s2 und s1 zwei zu den Zeiten t2,
t1 gemessene Wegstrecken sind. Entsprechend wäre dann Δt=t2-t1.
Im Idealfall lässt man Δs und Δt "unendlich klein"
werden und erhält so die Momentangeschwindigkeit v=Δs/Δt
für Δt→0. Oder mit dem limes-Zeichen geschrieben ("Limes",
lat., bedeutet "Grenze"):
![]()
Lässt man das Limes-Zeichen weg und ersetzt Δ durch d, nimmt die Momentangeschwindigkeit die Form
![]() an, d.
h. die Momentangeschwindigkeit ist der Differentialquotient oder die Ableitung des
Weges nach der Zeit.
an, d.
h. die Momentangeschwindigkeit ist der Differentialquotient oder die Ableitung des
Weges nach der Zeit.
Die Delta-Symbolik stammt von Gottfried Wilhelm Leibniz (1646-1716),
der etwa zeitgleich mit Newton, aber unabhängig von ihm, die Differential- und
Integralrechnung entwickelte. Newton bezeichnete die Ableitung
einer zeitabhängigen Größe y nach der Zeit mit einem darübergesetzten Punkt,
und das hat sich bis heute erhalten, so dass wir kürzer auch schreiben können:
![]()
Ganz entsprechend wird nun die Momentanbeschleunigung definiert,
oft auch nur Beschleunigung genannt:
![]()
![]()
Sie ist
die zweite Ableitung des Weges nach der Zeit; die
Momentangeschwindigkeit ist die erste Ableitung.
(Anmerkung zu den verwendeten Buchstabensymbolen: s steht für
"Strecke", t für lat. "tempus" = Zeit, v für lat. "velocitas"
= Geschwindigkeit und a für lat. "acceleratio" = Beschleunigung.)
*
Nun müssen wir, um das Folgende besser zu verstehen, darauf eingehen, wie man
Beschleunigungen misst – bei der Geschwindigkeit haben wir das
bereits getan.
Hierbei betrachten wir zunächst wieder einen Sonderfall: die Bewegung
soll geradlinig und die Beschleunigung a konstant sein. Dann folgt
(aus dem Hauptsatz der Analysis, nach dem die Umkehrung der Differentiation die
Integration ist) aus
![]()
v = a t + vo ,
wobei vo der Anfangswert der Momentangeschwindigkeit zur Zeit
t=0 ist.
Nochmalige Integration ergibt den zurückgelegten Weg
![]()
mit so als Anfangsstrecke zur Zeit t=0. Wählt man insbesondere vo = 0 und so = 0, bleibt übrig
s = a
t²/2 .
Aufgelöst nach a:
a = 2s/t² ,
verwendet man dies unter anderem für Versuche zum Freien Fall, bei denen der Luftwiderstand vernachlässigt werden kann. Dabei ergibt sich bei unterschiedlchen Messwertpaaren (s,t) für a ein fester Wert in der Nähe von 9,81 m/s2, der mit g bezeichnet wird und Fall- oder Erdbeschleunigung heißt.
*
Möchte man Versuche mit verschiedenen Beschleunigungswerten
anstellen, eignet sich dafür eine spezielle Fahrbahn. Sie besteht aus
einer Schiene, auf der möglichst reibungsfrei kleine Wagen hin- und herrollen
können. Die Fahrbahn wird waagerecht so ausgerichtet, dass sie sich nicht von
selbst in Bewegung setzen.
Seitlich an einem solchen Wagen ist ein Faden befestigt, der ebenfalls
waagerecht über eine Rolle am Ende der Schiene geleitet wird und dort
herunterhängt. An ihn kann man verschieden große Gewichtsstücke anhängen, die,
als Antriebskräfte wirkend, den Wagen unterschiedlich stark beschleunigen. Auch
die Masse des Wagens kann durch Auflegen von Gewichtsstücken verändert werden.
Bei Beschleunigungsversuchen mit der Fahrbahn ergibt sich, dass die
Beschleunigung proportional zur Antriebskraft und umgekehrt proportional zur
Masse des Wagens ist:
a = F/m
(F
steht für engl./franz. "force".)
Löst man dies nach F auf, entsteht die berühmte Newtonsche Gleichung
F = m a,
in
Worten: "Kraft gleich Masse mal Beschleunigung".
Obwohl diese Beziehung nach der vorstehenden kurzen Beschreibung experimentell
an einer geradlinigen Bewegung gefunden wurde, gilt sie auch bei
anderen Bewegungsformen, insbesondere für die Kreisbewegung. Vorausgesetzt wird
dabei, dass sich während der Bewegung die Masse m des Körpers nicht verändert.
Ist dies doch der Fall, tritt an die Stelle von F=m·a eine andere Gleichung,
die ebenfalls von Newton stammt.
Die Aussage "Kraft gleich Masse mal Beschleunigung" gehört zu den
Grundbestandteilen der Newtonschen Physik und wird deshalb auch
"Grundgleichung der Mechanik" genannt. Sie lässt sich auch auf den
Freien Fall anwenden. Die Antriebskraft, die einen fallenden Körper
beschleunigt, ist sein Gewicht G, so dass die Grundgleichung hierbei lautet:
G = m g ;
darauf komme ich später zurück.
*
Auch die oben erwähnte Zentripetalkraft FZ lässt
sich durch das Produkt m·a ausdrücken, wenn a die Zentripetalbeschleunigung bedeutet.
So können wir für die Zeile, in der der Term des Gravitationsgesetzes vorkommt,
schreiben:
ma =
ΓmM/r² .
Interessant hierbei ist, dass die Masse m der Mondfähre bei diesem
Problem keine Rolle spielt; sie kürzt sich aus der Rechnung heraus, und
es bleibt übrig:
a =
ΓM/r² .
Nun möchten wir aber aufgabengemäß nicht den Wert der Zentripetalbeschleunigung
a wissen, der sich leicht berechnen lässt, wenn ein bestimmter Bahnradius r
angenommen wird, sondern wollen einen Term für die Umlaufzeit der Fähre haben.
Deshalb müssen wir noch etwas weiter überlegen.
*
Dazu betrachten wir einen Kreis mit Radius r um den Ursprung und auf ihm einen
Punkt P mit den Koordinaten x = r cosφ, y = r sinφ. φ ist
der Winkel, den die Verbindungsstrecke zwischen P und dem Ursprung mit der
positiven x-Achse bildet. Nun soll P sich auf dem Kreis gegen den Uhrzeiger
gleichmäßig bewegen, d. h. φ soll sich proportional mit der Zeit
verändern:
φ = ω t.
ω
("Omega") heißt Winkelgeschwindigkeit, und der dafür
gewählte griechische Buchstabe erinnert als Gedankenstütze an das lateinische
w.
Wir schreiben also
x = r cosωt , y = r sinωt.
Einmal ableiten ergibt die x- und y-Komponente der Momentangeschwindigkeit bei
der gleichmäßigen Kreisbewegung
und ein zweites Mal die Komponenten der Zentripetalbeschleunigung:
Daraus folgt der Betrag:
und somit haben wir auch
Was lässt sich nun noch über ω sagen?
Wenn der Punkt P zur Zeit t=0 an der Stelle x=r, y=0 ist, dann ist er nach der
Umlaufzeit T wieder dort, d. h. es gilt r = r cosωT oder cosωT = 1.
Dies aber ergibt ωT = 2π und damit ![]()
Wenn wir das in die letzte Gleichung einsetzen, sind wir so gut wie fertig:
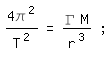
dies muss nur noch nach T aufgelöst werden. (T bedeutet die gesuchte Umlaufzeit der Mondfähre, r den Radius der Umlaufbahn und M die Masse des Mondes.)
*
Zum Abschluss zwei weitere Anwendungen der obigen Erkenntnisse, die
auch in der Schule behandelt werden können.
Die erste betrifft einen Körper der Masse m, zum Beispiel einen Stein, der auf
dem Erdboden liegt. Seine Gewichtskraft (kurz: sein Gewicht) beträgt mg, und
diese ist gleich der Gravitationskraft ΓmM/R2, wobei M jetzt
die Masse der Erde und R den Erdradius bedeuten. Auch hier kürzt sich, wie oben
bei der Fähre, die Masse m heraus, und übrig bleibt g = ΓM/R2.
Da g, Γ und R bekannt sind, kann man auf diese Weise die Masse der Erde bestimmen
– sicherlich ein erstaunliches Resultat!
(Historische Anmerkung: Newton kannte den Wert der Gravitationskonstanten
Γ noch nicht, jedenfalls nicht genau. Um ihn wenigstens
größenordnungsmäßig zu erfassen, ging er den umgekehrten Weg: er nahm an, dass
die Erde einigermaßen einheitlich aus den Gesteinen besteht, die an der
Erdoberfläche zu finden sind. Deren Dichte, die sich leicht messen lässt,
multiplizierte Newton mit dem Volumen der Erde – der Erdradius war längst
bekannt – und erhielt so einen Näherungswert für die Erdmasse. Den setzte er in
die obige Formel ein und erhielt so einen Näherungswert für Γ. Einen
wesentlich genaueren Wert, der in der Folge immer weiter verbessert wurde,
bestimmte 1789 der britische Chemiker und Entdecker des Wasserstoffs Henry
Cavendish (1731-1810) mit der von ihm erfundenen Gravitations-Drehwaage;
diese wird noch heute für Schulversuche verwendet.)
Unser zweites, abschließendes Anwendungsbeispiel ist ein sogenannter geostationärer Erdsatellit.
Seine Umlaufzeit beträgt 24 Stunden, so dass er ständig über einem festen Punkt
auf der Erdoberfläche bleibt. Welche Höhe h über dem Erdboden hat ein solcher
Satellit?
Wieder sei M die Erdmasse und R der Erdradius; dann ist in der obigen Gleichung
für die Umlaufdauer T der Mondfähre, die wir auch hier verwenden können, r = R
+ h. Für T = 24 Stunden ergibt sich h zu rund 36000 km. (Anmerkung: wer es
genau wissen will, darf nicht mit T = 24 Stunden, sondern muss mit etwas weniger
rechnen. Um nämlich festzustellen, wann sich die Erde exakt einmal um sich
selbst gedreht hat, muss man ihre Bewegung auf den Fixsternhimmel beziehen und
für T die Länge eines Sterntages nehmen. Dieser ist knapp 4 Minuten
kürzer als der Sonnentag mit 24 Stunden.)
Hans-Jürgen
|
Re: Umlaufzeit einer Mondfähre
und Weiteres |
|
|
|
Re:
Umlaufzeit einer Mondfähre und Weiteres |
|
|