Aus einer Mathematik-Olympiade im Jahre 1988 stammt folgende Aufgabe:

Zu beweisen ist: Wenn zwei natürliche Zahlen a unb b so gewählt werden, dass der Nenner des Bruches (a²+b²)/(1+ab) ein Teiler des Zählers ist, dann ist die entstehende natürliche Zahl stets eine Quadratzahl.

Die Aufgabe galt als sehr schwer und wurde nur von wenigen Teilnehmern gelöst. (Die Lösung wird unter dem Stichwort "Vieta Jumping" mehrfach im Internet beschrieben.)

Auch auf dem Matheplaneten spielte sie eine gewisse Rolle. Hier wurde nach Zahlenpaaren (a,b) gesucht, die den Bruch (a²+b²)/(ab+1) zu einer Quadratzahl machen; das ist etwas anderes als die ursprünglich gestellte Aufgabe. Der "Diskussionsfaden" (engl. thread ) war auf Grund eines sehr allgemein gehaltenen Ansatzes mit über vierzig Beiträgen besonders lang und nicht immer leicht zu durchschauen.

Hier beginne ich noch einmal ganz einfach und direkt. Sei a=n, b=cn; c,nÎℕ, dann ist

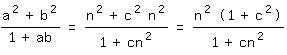
Wählt man c so, dass c²=cn² ist, dann gilt

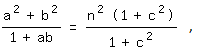
d. h., der Nenner des Bruches wird ein Teiler des Zählers, und der Bruch ist, wie gewünscht, eine Quadratzahl:

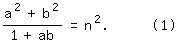
c²=cn² bedeutet c=n² und somit b= n³, d. h., a=n, b=n³ ist eines der gesuchten Zahlenpaare mit n als beliebig gewählter natürlicher Zahl.

Wegen der Symmetrie des Bruches in a unb b wird (1) auch beim Vertauschen der beiden Zahlen erfüllt: a=n³, b=n. Das ist trivial,
führt aber zu der Frage, ob es nicht auch ein solches Paar mit a=n³ und b¹n gibt.

Um darauf zu antworten, wird a=n³ in (1) eingesetzt und b neu berechnet. Die sich dabei ergebende quadratische Gleichung

b²-n⁵b+n⁶-n²=0   hat die Lösung


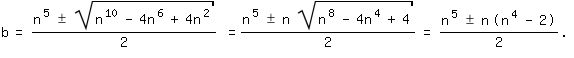
Gilt das Pluszeichen, wird b=n⁵-n, und ein zweites Lösungspaar ist a=n³, b=n⁵-n.



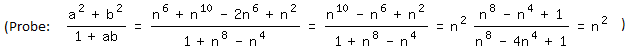
So kann man weiter fortfahren. Wir vertauschen wieder a und b und berechnen b durch Einsetzen von a=n⁵-n in (1). Dabei ergibt sich als drittes Lösungspaar: a=n⁵-n, b=n⁷-2n³.

In einem nächsten Schritt folgt entsprechend das vierte: a=n⁷-2n³, b=n⁹-3n⁵+n. (Bei ihm muss man erkennen, dass die unter der Wurzel stehende Summe n¹⁸-8n¹⁴+20n¹⁰-16n⁶+4n² das Quadrat von n⁹-4n⁵+2n ist.)

Die hier systematisch erhaltenen vier Lösungspaare (n;n³), (n³;n⁵-n), (n⁵-n;n⁷-2n³), (n⁷-2n³;n⁹-3n⁵+n) sind einzeln verstreut in dem genannten thread zu finden.

Für jedes n gibt es ein a und ein b, numeriert als a₁,a₂,a₃,. . .; b₁,b₂,b₃,. . . . Für die a_i (i=1,2,3,. . .) gilt: a_n+1=b_n , während bei den b_i keine einfache Regelmäßigkeit zu erkennen ist.

Die a_i sind rekursiv definiert. Das ist auch bei den b_i möglich. Mit genauem Hinschauen und ein wenig Probieren findet man: es ist b_n+1=n²b_n-a_n , was wegen a_n=b_n-1   b_n+1=n²b_n-b_n-1 ergibt. Damit lässt sich leicht als nächstes Beispiel (a₅,b₅)=(n⁹-3n⁵+n, n¹¹-4n⁷+3n³) berechnen; nichtrekursiv ist es sehr mühevoll. (Anmerkung: aus dem Vorstehenden folgt und wegen der Symmetrie der Aufgabe in a und b gilt auch noch a_n+1=n²a_n-a_n-1.)

Fortsetzung

Er hat eine unerwartete Besonderheit: wählt man die natürlichen Zahlen x und y so, dass auch er eine natürliche Zahl wird, dann ergibt sich immer dieselbe, und zwar die 5.
Das zeigt sich in der folgenden Tabelle:








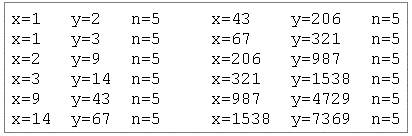
Zurück zur Themenübersicht , Teil 2