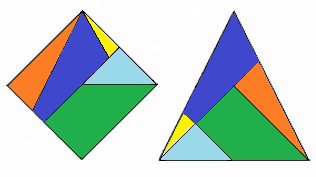
Über mögliche Lösungen der Aufgabe "Zerschneiden eines Quadrats"

Sei s die Länge eines Schenkels des gesuchten Dreiecks und g die Länge seiner Grundseite,
dann soll nach Voraussetzung gelten:
s/g=(√5 )/2 oder s²=5g²/4=g²+g²/4.
Andererseits gilt nach dem Satz von Pythagoras mit der Dreieckshöhe h:
s²=h²+g²/4, so daß aus beidem g=h folgt.

Der Flächeninhalt des Dreiecks ist somit gh/2=g²/2, und dieser soll gleich demjenigen des Quadrats sein.
Hat es die Seitenlänge a, so gilt weiter g²/2=a² und damit g = h =√2⋅a. Das bedeutet:
Die Grundseite und die Höhe des Dreiecks sind genauso lang wie die Diagonale des Quadrats.

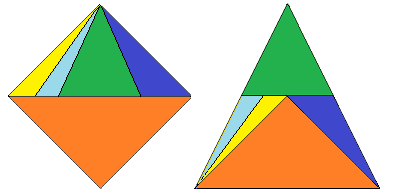
Diese Erkenntnis verwendete ich, wie es die folgende Bilderserie andeutet:


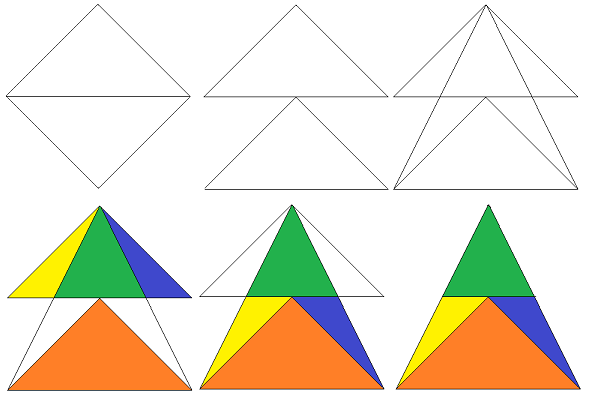
Das Dreieck am Ende erhält man, wenn das Quadrat so aufgeteilt wird:

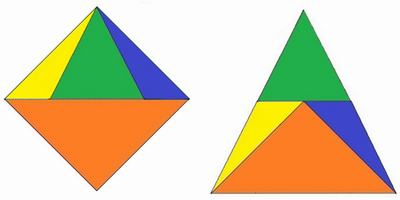
Hierzu sind drei Schnitte erforderlich und nicht vier, wie es in der Aufgabe heißt.

Allerdings enthält das Quadrat im Gegensatz zur Aufgabenstellung zwei zueinander
(ungleichsinnig) kongruente Teile. Das läßt sich vermeiden, indem man einen zerschneidet:

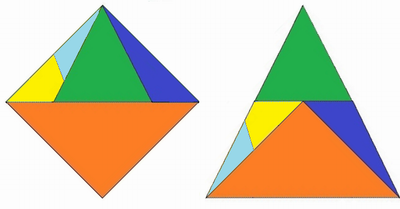
oder auch so:


Der vierte Schnitt kann beliebig ansetzen und schräg verlaufen; bei diesem Vorgehen hat die Aufgabe
unendlich viele Lösungen. –

Eine andere Art der Zerlegung des Quadrats durch vier Schnitte in fünf inkongruente Teile zeigt diese Figur: