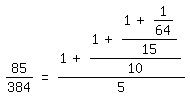Über Ketten- und Stammbrüche
Bei dem - leider erfolglosen - Versuch, eine von Buri gestellte Aufgabe zu lösen, suchte ich im Internet nach einem Zusammenhang zwischen unendlichen Kettenbrüchen und Reihen, fand aber außer ein paar Andeutungen kaum etwas dazu. Statt dessen stieß ich auf etwas wenig Bekanntes, über das hier kurz berichtet werden soll.
Es handelt sich um Kettenbrüche in aufsteigender Form, wie sie von dem berühmten Mathematiker, Physiker und Astronom Christiaan Huygens (1629 - 95) bei seinen Untersuchungen von Planetenbewegungen und Zahnrädern verwendet wurden.

(Das Bild stammt aus Wikipedia und ist "gemeinfrei".)
Später scheint man wieder davon abgekommen zu sein. Viel mehr in Gebrauch sind heute die wohlbekannten absteigenden Kettenbrüche wie etwa dieser:
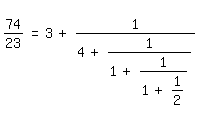
In der ausgedehnten Arbeit [1] über sie ist am Anfang von Abschnitt 2 ("Endliche Kettenbrüche") folgendes Beispiel eines aufsteigenden Kettenbruchs angeführt:
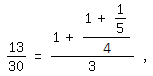
auf den im weiteren Verlauf nicht mehr zurückgegriffen wird.
Ein eigenes Beispiel soll zeigen, wie sich solch eine Form gewinnen läßt.


Interessant ist nun, daß sich das Beispiel von [1], wie bereits dort erwähnt, und auch unser zweites Beispiel als Summe von Stammbrüchen schreiben lassen, d. h. Brüchen mit dem Zähler 1 und natürlichem Nenner. Mit ihnen rechneten gern die alten Ägypter. Es gilt
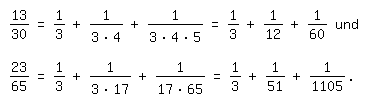
Die Darstellung von Brüchen durch Stammbruchsummen ist nicht eindeutig, vgl. [2] mit einem diesbezüglichen, interaktiven Programm und weiteren Ausführungen dazu.
Ein gesundes, gutes Neues Jahr 2010 wünscht allen Leserinnen und Lesern
Hans-Jürgen.
[1] Algorithmen für regelmäßige Kettenbrüche
[2] Die Ägyptische Darstellung von Brüchen mit Stammbrüchen
|
Re: Über Ketten- und
Stammbrüche
von Bernhard
am Mo. 04. Januar 2010 00:51:11
|
|
Hallo Hans-Jürgen!
Das ist schon interessant, was Du da berichtest. Auf die Idee, die
Kettenbrüche in die Zähler zu verlegen, wäre ich nie gekommen.
Besonders schön ist auch Dein zweiter Link über die Darstellung von Brüchen
mit Stammbrüchen. Ich habe zwar gewußt, daß diese nicht eindeutig ist, aber
daß es teilweise so viele geben kann, hatte ich nicht geahnt.
In diesem Zusammenhang noch zwei Fragen:
1.) Kann man die Zahl solcher aller Darstellungen für einen bestimmten Bruch
berechnen (nicht ausprobieren!)?
2.) Gibt es überhaupt Brüche, die sich nur auf eine einzige Art als
Summe von (verschiedenen) Stammbrüchen darstellen lassen?
3.) Könnte man eine eindeutige Darstellung bekommen, wenn man bestimmte
Einschränkungen vornimmt? Ich denke insbesondere daran, daß man z.B. nur
Primzahlen im Nenner zuläßt, aber dafür die gleiche Summanden auch mehrmals
auftauchen dürfen.
Vielen Danke für Deine Anregungen!
Bernhard
|
|
Re:
Über Ketten- und Stammbrüche
von Hans-Juergen
am Mo. 04. Januar 2010 10:55:34 http://www.hjcaspar.de
|
|
Ergänzungen:
1. Der aufsteigende Kettenbruch unseres letzten Beispiels läßt sich in einer
Zeile übersichtlich so schreiben:
23/65 = (1+(1+(1+1/65)/22)/17)/3 .
2. Während man für einen anderen Bruch, nämlich 85/384, mit Hilfe des
Interaktiv-Programms in [2] diese Darstellung als Summe von Stammbrüchen
erhält:
85/384=1/5+1/47+1/12892+1/290843520 ,
ergibt sich über den Kettenbruch
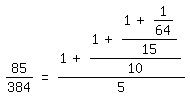
85/384=(1+(1+(1+1/64)/15)/10)/5
= (1+(1+(1+1/64)/15)/10)/5 für ihn:
85/384=1/5+1/50+1/750+1/48000
mit erfreulich "glatten" Nennern.
Hans-Jürgen
|
|
Re:
Über Ketten- und Stammbrüche
von Kay_S
am Mo. 04. Januar 2010 22:37:17 http://www.kay-schoenberger.de
|
|
Es gibt unendlich viele Stammbruchentwicklungen. Denn hat man eine Entwicklung
a/b = 1/m + ... + 1/n (1/n ist der kleinste Bruch)
gefunden, so bekommt man mit 1/n = 1/(3n) + 2/(3n) eine neue Zerlegung, wobei
2/(3n) nach dem Greedy-Prinzip (wie im Beitrag von Hans-Juergen) weiter
zerlegt wird (der Greedy-Algo bricht immer ab, da der Zähler verringert
wird). Zu den ägyptischen Brüchen ist vielleicht auch das Applet auf meiner
Webseite (Link) interessant :-)
|
Zurück zur Themenübersicht, Teil 2