Über Kettenbrüche
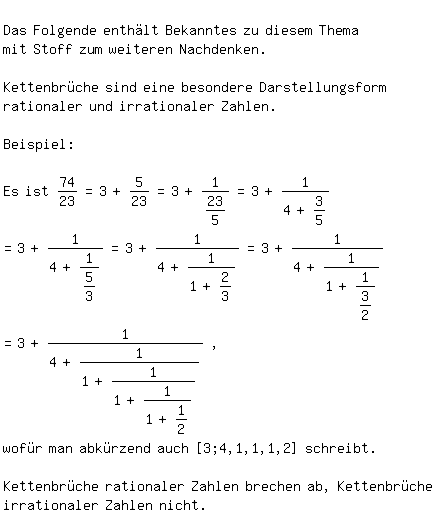
Darüber hinaus sind Kettenbrüche von Lösungen quadratischer Gleichungen
periodisch, wie das folgende Beispiel zeigt:
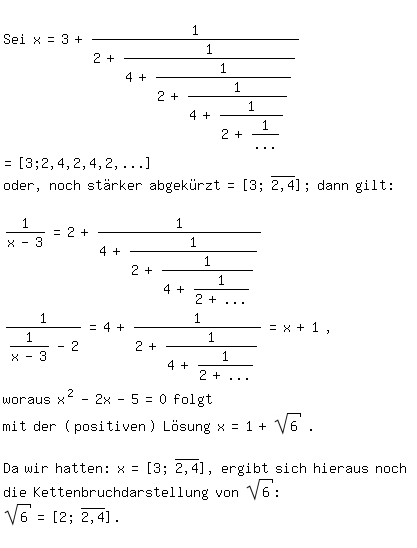
Mit dem von buri zitierten Kettenbruch-Generator kann man sich
weitere Quadratwurzeln als Kettenbrüche zeigen lassen.
Wir sahen, daß ein periodischer Kettenbruch auf eine quadratische
Gleichung führt. Geht man umgekehrt von einer solchen aus,
z. B. von
ax²-bx-c=0, dann ist dies gleichbedeutend mit
x²=(b/a)x+c/a, und durch beiderseitiges Dividieren durch x<>0
ergibt sich:

Keinen Hinweis fand ich darauf, wie man Kubikwurzeln als Kettenbruch
schreiben kann. Dabei muß so etwas möglich sein, fragt sich nur, wie.
In dem Buch "Zahlentheoretische Kostproben" von T. Kempermann
steht ohne Begründung der Anfang für die Kubikwurzel von 3:
[1;2,3,1,4,1,5,...].
Dieser Kettenbruch ist unperiodisch wie bei allen Kubikwurzeln (wird gesagt),
und die letzten angegebenen fünf Ziffern sehen aus wie der Anfang
von Pi: 3,1415... (Welche Ziffer mag wohl als nächste kommen?)
Pi selber, als Kettenbruch geschrieben, ist unregelmäßig: [3;7,15,1,292,1,1,1,2],
im Gegensatz zur Eulerschen Zahl, für die gilt:
e=[2;1,2,1,1,4,1,1,6,1,1,8,1,1,10,...].
Die unregelmäßige Kettenbruchdarstellung von Pi ergibt sich nur, wenn
die "Zähler" der Teilbrüche wie in den obigen Beispielen alle gleich 1
sind. Hebt man diese Beschränkung auf, gibt es für Pi mehrere schöne
und regelmäßige Kettenbruchentwicklungen wie z. B. diese:
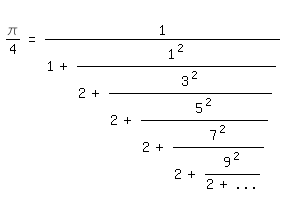
Sie stammt wie die für e von Euler. "Empirisch", so heißt es in der einschlägigen
Literatur, wurde sie bereits von Lord Brouncker (1630-1684) gefunden; Euler
begründete sie hundert Jahre später mit Hilfe der Arkustangensfunktion.
(Brouncker war kein Mathematiker, sondern vor allem Politiker und Gründer
sowie erster Präsident der Royal Society. Er war befreundet mit John Wallis,
dem wir die Darstellung von Pi durch ein unendliches Produkt verdanken.)
Hans-Jürgen
(16.3.04)
Aus der anschließenden Diskussion:

Zurück zur Themenübersicht