Die Kettenlinie als Minimalproblem

Im folgenden wird die Gleichung der Kettenlinie hergeleitet. Diese parabelähnliche Kurve hat ihren Namen von einer unter ihrem Eigengewicht durchhängenden Kette, doch tritt sie auch bei Seilen in Erscheinung und läßt sich zum Beispiel an Hochspannungsleitungen beobachten.

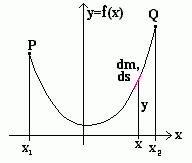
Hängt man ein Seil locker zwischen zwei Punkten P und Q auf (s. Abb.) und läßt es dann los, kommt es nach einigen unregelmäßigen Bewegungen zur Ruhe. Seine potentielle Energie wird dabei minimal. Begründung: Solange Teile des Seils noch fallen, nimmt deren potentielle Energie ab, und wenn sich nichts mehr bewegt, kann sie sich nicht weiter verringern.

Ein kleines Seilstück der Masse dm an der Stelle x hat die Höhe y und somit die potentielle Energie dW = g y dm
(g = Erdbeschleunigung). Das ganze Seil enthält also die potentielle Energie


Wenn das Seil aus homogen verteiltem Material besteht, ist der Quotient dm/ds=γA konstant; ds bedeutet dabei das Linienelement √(1+y'²)dx, γ die Massendichte und A die Querschnittsfläche des Seils. Seine potentielle Energie ist damit


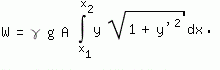
Von allen Kurven gleicher Länge, die zwischen den Punkten P und Q verlaufen können und durch Gleichungen der Form y = F(x) beschrieben werden, soll nun diejenige gefunden werden, bei der der Wert des Integrals W minimal wird. Diese Aufgabe aus der Variationsrechnung, symbolisch durch δW = 0 abgekürzt, führt auf die Euler-Lagrangesche partielle Differentialgleichung



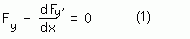
mit F(x,y,y')=y√(1+y'²) in unserem Fall.

(Anmerkung: Über die Entstehung dieser berühmten partiellen Differentialgleichung berichtete vor kurzem ausführlich SplendourMN im Zusammenhang mit der Brachistochrone.)

Aus (1) ergibt sich die gewöhnliche Differentialgleichung (Rechnung s. u.)

1 + y'² - y y'' = 0 (2)

Wegen (sinh x)' = cosh x, (cosh x)' = sinh x und cosh²x - sinh²x = 1 wird sie durch y = cosh x erfüllt. Die allgemeine Lösung mit zwei Integrationskonstanten a, b lautet y = a cosh (x/a+b). Für b=0 wird daraus, anders geschrieben,

y = a (e^x/a+e^-x/a)/2. (3)

Dies ist die Gleichung der Kettenlinie, wie sie nach [1] zuerst von Leibniz angegeben wurde.

Vor Leibniz hatten sich andere namhafte Mathematiker und Physiker darum bemüht, unter ihnen Galilei, Jakob und Johann Bernoulli, Huygens und Pascal. Wie Leibniz zu seiner Lösung kam, konnte ich nicht feststellen. In [1] gibt es lediglich den kurzen Hinweis, er hätte dazu die "logarithmische Kurve" benutzt, mit dem man nicht viel anfangen kann.

Die Anwendung der Variationsrechnung auf die Kettenlinie ist "schweres Geschütz". Vielfach findet man statt dessen einen Ansatz mit Kräftezerlegung, z. B. in [2]. Dort ist ohne Begründung von einer konstanten, in waagerechter Richtung wirkenden Kraftkomponente die Rede, die ich nicht verstehe. Auch ergibt sich dabei eine andere Differentialgleichung, nämlich


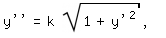
die allerdings ebenfalls die Lösung (3) hat.

Anmerkung: in [3] wird die Konstanz der Horizontalkomponente verständlich erklärt.

Literatur:

[1] Hartmut Hecht: Gottfried Wilhelm Leibniz, Mathematik und Naturwissenschaften im Paradigma der Metaphysik, B. G. Teubner, Stuttgart/Leipzig, 1992, S. 58

[2] http://mathsrv.ku-eichstaett.de/MGF/homes/grothmann/Projekte/Kettenlinie/loesung.html

[3] http://www.mathe-seiten.de/kettenlinie.pdf


Herleitung von (2) aus (1):



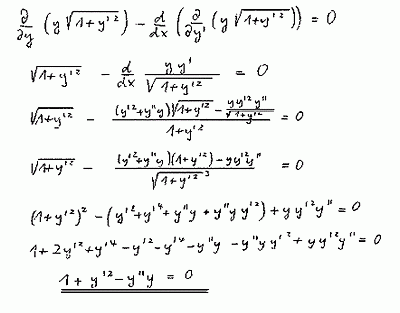
Nachtrag
Der Kettenlinie begegnet man an taubenetzten Spinnenfäden, Absperrungen und in der Architektur:
[*]     
Rechts: Gateway Arch (Wikipedia, s. speziell den Abschnitt "Bauwerke und Einrichtungen").

Auf der Gateway-Wikipediaseite wird der Freiheitsbogen des ukrainischen Volkes in Kyjiw erwähnt.
Er soll den Regenbogen symbolisieren und folgt nicht der Kettenlinie.

Sie fotografierte ich schräg von der Seite in einem griechischen Kloster als Glockenstrang:



Zurück zur Themenübersicht