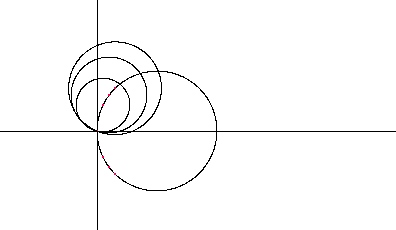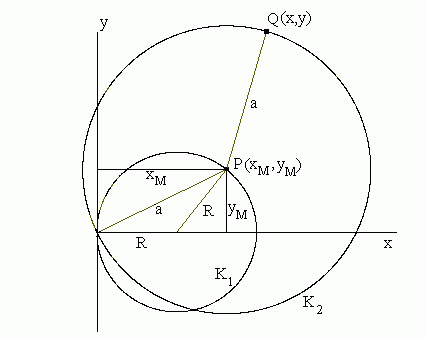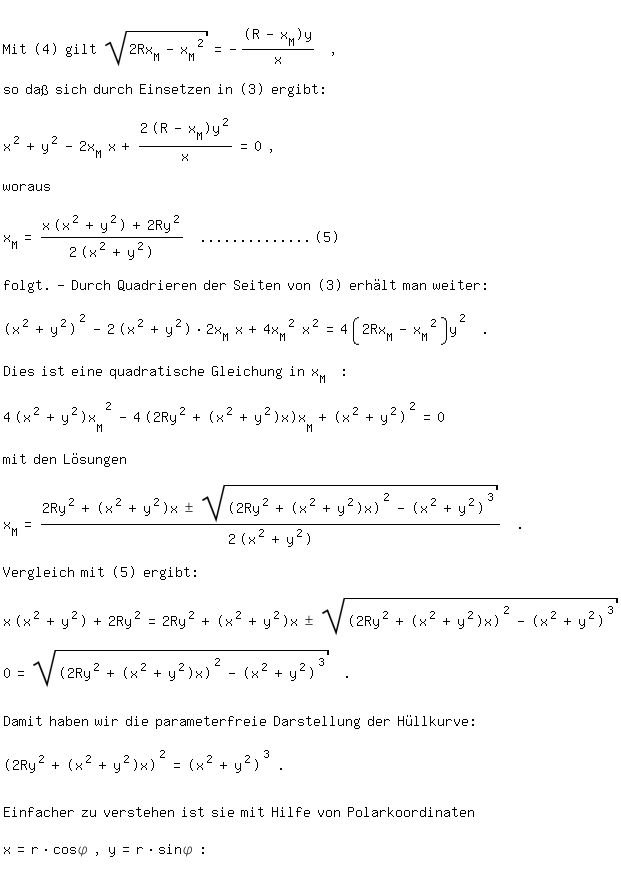Die Kardioide als Hüllkurve

Bei einer früheren Gelegenheit [1] beschäftigte ich mit den Einhüllenden von Kurvenscharen. Hier folgt ein weiteres Beispiel, das wahrscheinlich schon längst bekannt ist, mir aber bisher noch nicht auffiel. (Ich habe auch nicht danach gesucht, weder in Büchern noch im Internet.)

Wählt man auf einem Kreis, dessen Mittelpunkt auf der x-Achse liegt und der durch den Ursprung geht, beliebige Punkte,

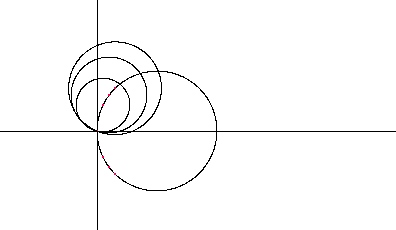
und schlägt um sie Kreise, die ebenfalls durch den Ursprung gehen,

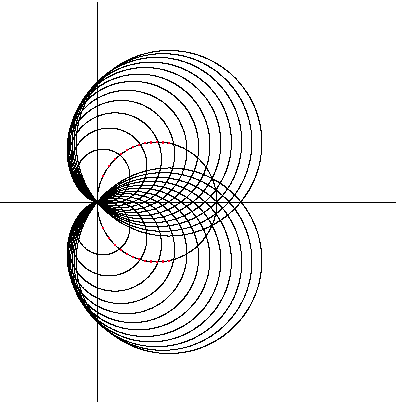
so ist die Einhüllende der so entstehenden Kreisschar eine Kardioide:

Beweis:

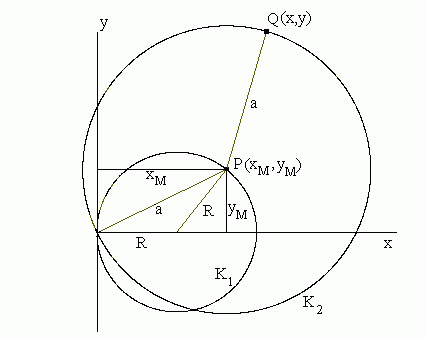
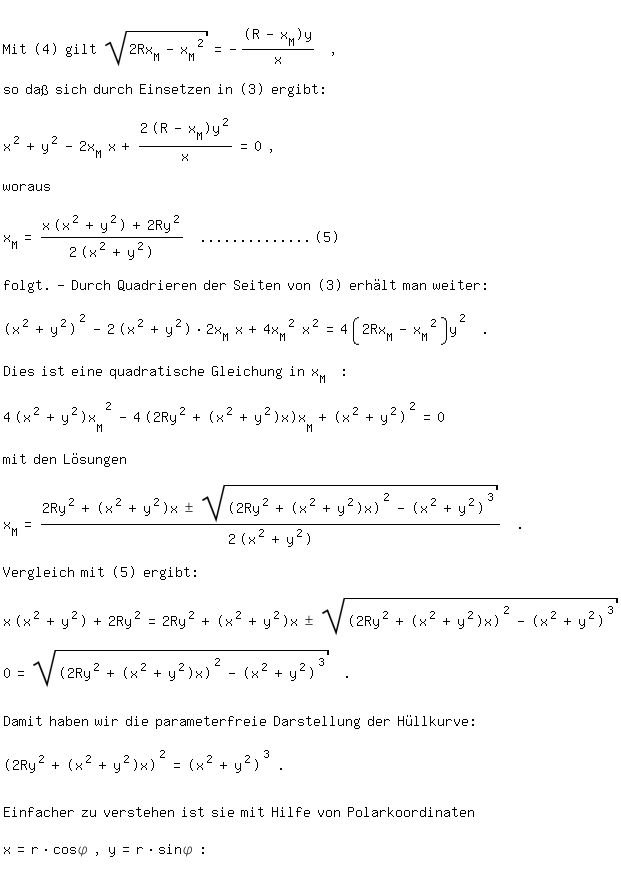
[1] Über Hüllkurven

Hans-Jürgen

Re: Die Kardioide als Hüllkurve
von Diophant am Do. 03. September 2009 17:56:31

Lieber Hans-Jürgen,

manchmal findet man ja auch draußen in der Natur etwas besonders schönes: eine schöne Blume, einen schönen Stein oder dergleichen.
Auf dem Matheplaneten gibt es das auch bisweilen. Deine Artikel und ganz besonders dieser gehören dazu!

Liebe Grüße, Johannes

Re: Die Kardioide als Hüllkurve
von rambo3 am Do. 03. September 2009 21:44:02

Schön gesagt, ich find ihn auch sehr interesant

Re: Die Kardioide als Hüllkurve
von zimti am Fr. 05. November 2010 12:32:21

hallo :)
der Artikel hat mit sehr geholfen!
mir ist nur nicht ganz klar wie man bei der herleitung mit polarkoordinaten vom 1. auf den 2. schritt kommt!
Kann mir jemand erklären was da gemacht wurde?
Danke :)

Re: Die Kardioide als Hüllkurve
von Hans-Juergen am Fr. 05. November 2010 20:09:02 http://www.hjcaspar.de

Hallo zimti,

ich will Dir gerne erklären, was da gemacht wurde,
wenn Du mir sagtst, was Du unter dem 1. und dem
2. Schritt verstehst. Wir können uns darüber auch
per PN ("Private Nachricht") unterhalten. Klicke
dazu oben auf meinen Namen und gehe dann auf die
sich öffnende Seite ganz unten.

Gruß,
Hans-Jürgen

Zurück zur Themenübersicht, Teil 2