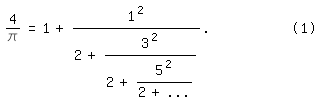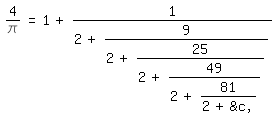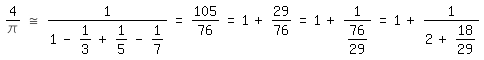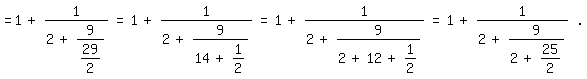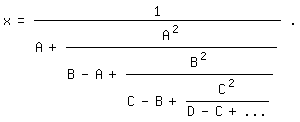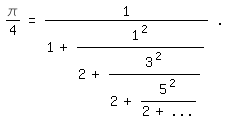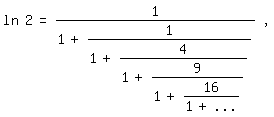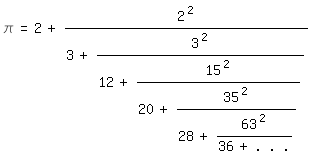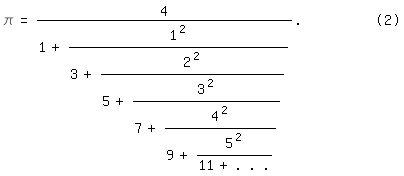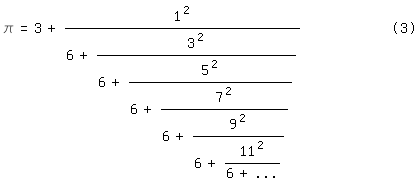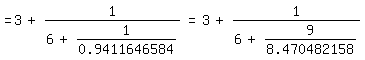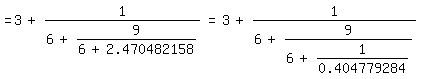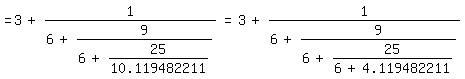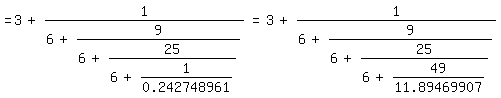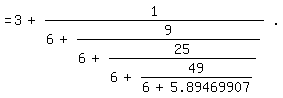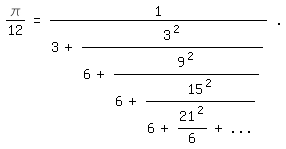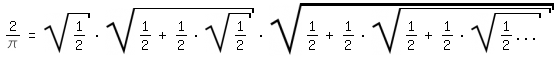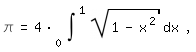Über einige irreguläre Kettenbrüche

Kettenbrüche sind im Internet und so auch auf dem Matheplaneten ein reizvolles Thema. Dabei wird den regulären Kettenbrüchen, deren Teilzähler alle gleich 1 sind, weit mehr Aufmerksamkeit geschenkt als den irregulären, bei denen dies nicht der Fall ist. Über diese habe ich im folgenden einiges zusammengetragen.

Von dem englischen (oder irischen?) Mathematiker Lord William Brouncker (1620 bis 1684), einem Gründungsmitglied und späterem Rektor der Royal Society, stammt der Kettenbruch
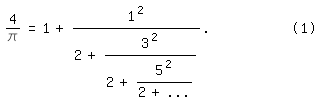
http://fed.matheplanet.com/mprender.php?stringid=7115009fed-Code ausblenden

4/\pi=1+1^2/(2+3^2/(2+5^2/(2+...))).| (1)


Veröffentlicht wurde er 1655. Dreißig Jahre später, 1685, schrieb John Wallis (1616 bis 1703) darüber:

"Wir sagen daher; dass sich der Kreis zum Quadrat seines Durchmessers verhält wie 1 zu
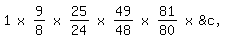
http://fed.matheplanet.com/mprender.php?stringid=7106765fed-Code ausblenden

1 x|9/8|x|25/24|x|49/48|x|81/80|x &c,

unendlich oft. Oder wie 1 zu
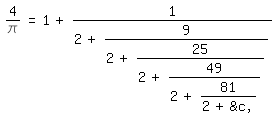
http://fed.matheplanet.com/mprender.php?stringid=7106788fed-Code ausblenden

4/\pi=1+1/(2+9/(2+25/(2+49/(2+81/(2+&c,))))

unendlich oft. Wie diese Annäherungen erhalten wurden . . . wäre hier zu lang zu berichten; aber kann von denen eingesehen werden, die die Abhandlung heranziehen möchten." [1] (&c - Abkürzung für et cetera = und so weiter.)

Brounckers Kettenbruch sei, so wird mehrfach erwähnt, durch Umformung des Wallis-Produkts entstanden - wie, wisse man nicht. Manche schreiben, Brouncker habe ihn durch Probieren ("empirisch") gefunden. Ohne Rückgriff auf das Wallis-Produkt ist folgendes möglich:

Nach der Leibnizreihe gilt
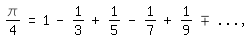
http://fed.matheplanet.com/mprender.php?stringid=7106984fed-Code ausblenden

\pi/4=1-1/3+1/5-1/7+1/9-+ ... ,

so daß, wenn man sich auf die ersten vier Glieder beschränkt, folgt:
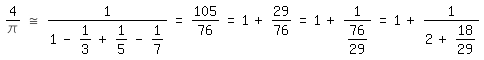
http://fed.matheplanet.com/mprender.php?stringid=7108077fed-Code ausblenden

4/\pi ~=1/(1-1/3+1/5-1/7)=105/76=1+29/76=1+1/(76/29)=1+1/(2+18/29)


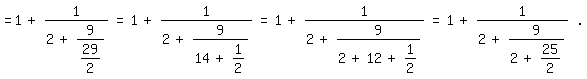
http://fed.matheplanet.com/mprender.php?stringid=7108122fed-Code ausblenden

=1+1/(2+9/(29/2))=1+1/(2+9/(14+1/2))=1+1/(2+9/(2+12+1/2))=1+1/(2+9/(2+25/2))|.

Das ist der Anfang des Brounckerschen Kettenbruchs.

Bewiesen hat die Beziehung (1) knapp hundert Jahre nach ihrer Entdeckung Leonhard Euler in seiner 1748 lateinisch geschriebenen Introductio in analysin infinitorum [2]. Dort zeigte er allgemein, daß sich eine unendliche Reihe der Form
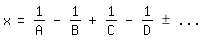
http://fed.matheplanet.com/mprender.php?stringid=7109483fed-Code ausblenden

x=1/A-1/B+1/C-1/D+-. . .

in dieser Weise als Kettenbruch schreiben läßt:
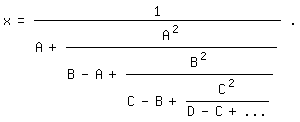
http://fed.matheplanet.com/mprender.php?stringid=7110640fed-Code ausblenden

x=1/(A+A^2/(B-A+B^2/(C-B+C^2/(D-C+ . . .))))|.


Speziell ergibt sich daraus für die Leibnizreihe mit A=1, B=3, C=5, D=7, . . . :
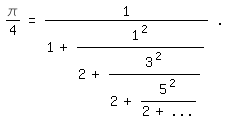
http://fed.matheplanet.com/mprender.php?stringid=7110639fed-Code ausblenden

\pi/4=1/(1+1^2/(2+3^2/(2+5^2/(2+...))))|.

Das ist der Kehrwert des Brouncker-Kettenbruchs.

Auch dieser Kettenbruch stammt von Euler:
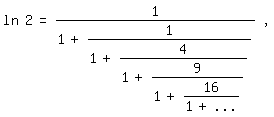
http://fed.matheplanet.com/mprender.php?stringid=7110642fed-Code ausblenden

ln| 2 = 1/(1+1/(1+4/(1+9/(1+16/(1+...)))))|,

für den in der o. g. Reihe A=1, B=2, C=3, D=4, . . . gilt.

Mit der Leibnizreihe kann man ein wenig experimentieren und sie z. B. in dieser Form schreiben:
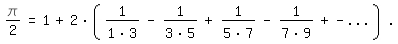
http://fed.matheplanet.com/mprender.php?stringid=7121923fed-Code ausblenden

\pi/2=1+2*(1/(1*3)-1/(3*5)+1/(5*7)-1/(7*9) + - ...)|.


Der daraus entstehende Kettenbruch mit verschiedenen Zahlen anstelle der 2 am Zeilenanfang:
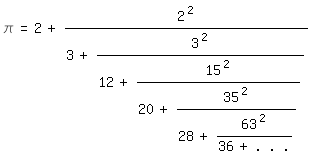
http://fed.matheplanet.com/mprender.php?stringid=7121974fed-Code ausblenden

\pi=2+2^2/(3+3^2/(12+15^2/(20+35^2/(28+63^2/(36+. . .)))))|

ist vor allem wegen der großen Quadratzahlen sehr unhandlich im Vergleich zu dem in [3] wiedergegebenen von Johann Heinrich Lambert (1728 bis 1777):

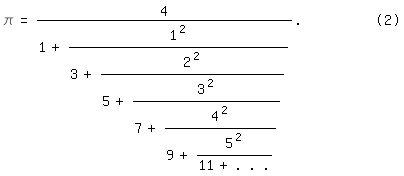
http://fed.matheplanet.com/mprender.php?stringid=7119775fed-Code ausblenden

\pi=4/(1+1^2/(3+2^2/(5+3^2/(7+4^2/(9+5^2/(11+. . .)))))).| (2)


Lambert war vielseitig produktiv, nicht nur in der Mathematik, vgl. [4]. Wie Euler beschäftigte auch er sich intensiv mit den Kettenbrüchen, wobei seine im Internet wiedergegebenen Untersuchungen besser zu lesen sind als diejenigen Eulers. Zu vermuten wäre ein Beweis für (2) in [5], evtl. auch [6], doch habe ich ihn dort nicht gefunden.

Der folgende Kettenbruch
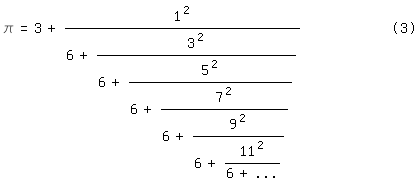
http://fed.matheplanet.com/mprender.php?stringid=7129214fed-Code ausblenden

\pi = 3 + 1^2/(6+3^2/(6+5^2/(6+7^2/(6+9^2/(6+11^2/(6+...))))))| (3)

wurde 1999 von dem amerikanischen Mathematiker L. J. Lange veröffentlicht. In [3] wird erwähnt, daß er auf Euler zurückgeht. In [7] ist die Einleitung zu Langes Arbeit wiedergegeben; um den Beweis selbst zu sehen, muß man sich anmelden und einiges mehr.

Wenn π bereits bekannt ist, kann man den Anfang etwa von (3) so gewinnen:

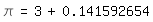
http://fed.matheplanet.com/mprender.php?stringid=7116509fed-Code ausblenden

\pi=3+0.141592654


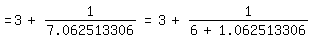
http://fed.matheplanet.com/mprender.php?stringid=7116471fed-Code ausblenden

=3+1/7.062513306=3+1/(6+1.062513306)


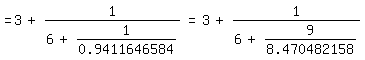
http://fed.matheplanet.com/mprender.php?stringid=7116467fed-Code ausblenden

=3+1/(6+1/0.9411646584)=3+1/(6+9/8.470482158)


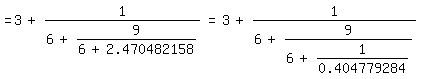
http://fed.matheplanet.com/mprender.php?stringid=7116498fed-Code ausblenden

=3+1/(6+9/(6+2.470482158))=3+1/(6+9/(6+1/0.404779284))


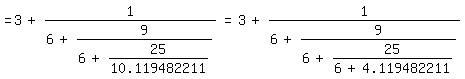
http://fed.matheplanet.com/mprender.php?stringid=7116500fed-Code ausblenden

=3+1/(6+9/(6+25/10.119482211))=3+1/(6+9/(6+25/(6+4.119482211)))


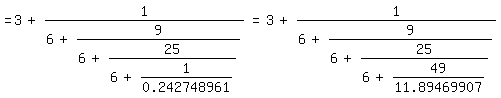
http://fed.matheplanet.com/mprender.php?stringid=7116501fed-Code ausblenden

=3+1/(6+9/(6+25/(6+1/0.242748961)))=3+1/(6+9/(6+25/(6+49/11.89469907)))


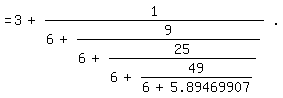
http://fed.matheplanet.com/mprender.php?stringid=7121932fed-Code ausblenden

=3+1/(6+9/(6+25/(6+49/(6+5.89469907))))|.



Natürlich ersetzt eine solche Rechnung keinen allgemeinen Beweis, denn ob es nach diesem Schema (vorne die 6, rechts aufeinander folgende, ungerade Quadratzahlen) immer so weiter geht, ist nicht sicher.

Hans-Jürgen

Nachtrag (28.2.):

Durch Multiplikation der Leibnizreihe mit 1/3:
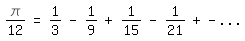
http://fed.matheplanet.com/mprender.php?stringid=7129152fed-Code ausblenden

\pi/12=1/3-1/9+1/15-1/21+ - ...

entsteht mit A=3, B=9, C=15, D=21 usw. in der obigen Eulerschen Gleichung der Kettenbruch
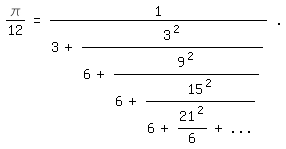
http://fed.matheplanet.com/mprender.php?stringid=7129192fed-Code ausblenden

\pi/12=1/(3+3^2/(6+9^2/(6+15^2/(6+21^2/6+...))))|.
fed-Code ausblenden

Durch die einheitliche 6 am Anfang ab der zweiten Zeile unter dem Hauptbruchstrich ähnelt er dem Kettenbruch (3), läßt sich aber anscheinend nicht in diesen umformen und konvergiert außerdem wesentlich schlechter als er. Wie (3) entsteht, bleibt offen und bietet, ohne Suchen im Internet oder in Büchern, weiter Anlaß zu eigenem Nachdenken.


[1] J.Wallis 1685, A Treatise of Algebra, S. 318, zitiert in
http://www.science-shop.de/sixcms/media.php/370/Leseprobe.749173.pdf, S. 73
[2] L. Euler, Introductio in analysin infinitorum; deutsche Übersetzung hier: http://www.math.dartmouth.edu/~euler/docs/originals/E101capitel16.18.pdf, S. 301ff.
[3] http://www.springerlink.com/content/g980446186625034
[4] http://www.kuttaka.org/~JHL/WerkeThem.html
[5] http://www.kuttaka.org/~JHL/L1770a_3.pdf, lange PDF-Datei (ca. 8 MB)
[6] http://www.kuttaka.org/~JHL/L1770a_5.pdf (ca. 3 MB)
[7] The American Mathematical Monthly, Vol. 106, No. 5 (May, 1999), pp. 456-458
http://www.jstor.org/pss/2589152 Anzeige Sonderband zu Ehren Langes: http://www.ams.org/bookstore-getitem/item=CONM-236




Re: Über einige irreguläre Kettenbrüche
von Wally am Sa. 26. Februar 2011 20:06:00 http://silber-ruecken.de/ghhp/Peter


Lieber Hans-Jürgen,

vielen Dank für eine tolle Idee für einen Seminarvortrag. Wenn ich schöne Themen sehe, bin ich immer dankbar - wie jetzt :)

Wally

 

Re: Über einige irreguläre Kettenbrüche
von Bernhard am Mo. 28. Februar 2011 22:30:29


Hallo Hans-Jürgen!

Es sind wirklich immer, faszinierende Sachen, die Du da hervorholst un uns anschaulich erläuterst. Der direkte Zusammenhang bzw. die Ableitung der Leibnizreihe und einem Kettenbruch war mir bis dato nicht bekannt. Ich wußte nur, daß es für die Darstellung von Pi beide Möglichkeiten gibt.
Ich frage mich langsam, auf wieviele Arten man Pi noch darstellen kann? Wenn man mal von trivialen Umformungen durch einfache Addition oder Multiplikation absieht.

Bernhard

 

Re: Über einige irreguläre Kettenbrüche
von Wauzi am Mo. 28. Februar 2011 23:02:03


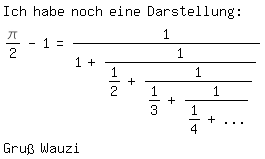
http://fed.matheplanet.com/mprender.php?stringid=7130256fed-Code ausblenden

Ich habe noch eine Darstellung:
\pi/2-1=1/(1+1/(1/2+1/(1/3+1/(1/4+...))))
Gruß Wauzi

Re: Über einige irreguläre Kettenbrüche
von Anonymous am Mo. 28. Februar 2011 23:04:11


Bieten Kettenbrüche eigentlich auch eine verbesserte Auswertbarkeit? Oder habe sie nur ästhetische Qualität? Ich sehe nämlich nicht, wie man die Kettenbrüche konkret berechnen kann. Geht das rekursiv?

 

Re: Über einige irreguläre Kettenbrüche
von Bernhard am Mo. 28. Februar 2011 23:37:27


Hallo Anonymus!

Ich kann Dich gut verstehen. Sie Kettenbrüche sehen imposant aus und es ist faszinierend, daß sie überhaupt funktionieren.
Aber ich weiß auch nie ganz genau, wo ich anfangen soll - oben oder unten - vorne oder hinten? :-?

Bernhard

 

Re: Über einige irreguläre Kettenbrüche
von Hans-Juergen am Di. 01. März 2011 16:06:07 http://www.hjcaspar.de


Hallo Bernhard und Anonymus,

man fängt hinten (unten) an, beim Lambertschen Kettenbruch (2) also mit 25/11, und arbeitet sich bis nach vorne durch. Bei Verwendung des Taschenrechners und dessen Quadrat- und Kehrwerttaste geht das bequem und rasch. (Im eigentlichen Wortsinn - von lat. recurrere=zurückgehen - ist das rekursiv, wonach gefragt wurde.)

Was die Möglichkeiten, Pi angenähert zu berechnen, betrifft, so gibt es davon Dutzende, vgl. z. B. das Buch "PI" mit dieser MP-Rezension.

Während das Wallis-Produkt nur eine einzige Grundrechenart, die Multiplikation, verwendet, enthalten die anderen Formeln ein Mix von +, -, ⋅ und :, aber auch "höhere" Rechenarten wie bei Vietas Kettenwurzel
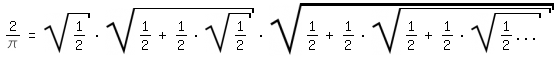
http://fed.matheplanet.com/mprender.php?stringid=7132090fed-Code ausblenden

2/\pi=sqrt(1/2)*sqrt(1/2+1/2*sqrt(1/2))*sqrt(1/2+1/2*sqrt(1/2+1/2*sqrt(1/2...)|/fedoff


von 1593, also noch rund sechzig Jahre vor dem Brouncker-Kettenbruch, und sogar diese:
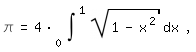
http://fed.matheplanet.com/mprender.php?stringid=7132016fed-Code ausblenden

\pi=4*int(sqrt(1-x^2),x,0,1)|,

letztere mit einer einfachen, anschaulichen Bedeutung.

Und um noch einmal auf die Kettenbrüche zurückzukommen: platzsparend kann man sie in einer Zeile z. B. so schreiben (auch anderes ist gebräuchlich):
x=a/(b+c/(d+e/(f+g/h...))).

Ein Gegenstück hierzu entsteht, wenn der Bruchstrich durch den Malpunkt ersetzt wird:
y=a⋅(b+c⋅(d+e⋅(f+g⋅(h...)))) ; x und y bedeuten nicht dasselbe.

Wie man darauf kommt und im Falle von Pi nutzbringend anwenden kann, habe ich vor zehn Jahren hier, als man noch öfter in Pascal programmierte, beschrieben.

Viele Grüße,
Hans-Jürgen

Re: Über einige irreguläre Kettenbrüche
von Dixon am Di. 01. März 2011 20:08:05


Hallo zusammen,

man kann Kettenbrüche auch "von vorn" berechnen, man benötigt dazu die
beiden vorhergehenden Näherungen. Formeln finden sich z.B. bei
wikipedia.
Es gibt gewisse Zahlen, für die können geschlossene Formeln zur
Bestimmung der Kettenbruchentwicklung angegeben werden. Das betrifft
z.B. Wurzeln aus natürlichen Zahlen, deren Kettenbruchentwicklung ist
periodisch. Das erkannte schon Euler.
Für einige andere Zahlen, so für e und e^2, lassen sich geschlossene
Formeln ableiten. Die Kettenbrüche sind nicht periodisch, aber
regelmäßig.
Näherungen aus Kettenbrüchen sind die besten Approximationen von
reellen Zahlen durch rationale. So sind die beiden bekannten
Näherungen für Pi 22/7 und 355/113 (und die Inder sollen noch bessere
gekannt haben) durch an bestimmten Stellen abgebrochene
Kettenbruchentwicklungen darstellbar. Die Genauigkeit hängt mit der
Größe des Nenners der Entwicklung zusammen, sie ist besser als der
Kehrwert des Quadrates des Nenners (355/113=3,1415929...).
In der Anwendung können sie auch interessante Einblicke liefern.
So ergibt die Entwicklung des Verhältnisses (Länge des synodischen
Monats)/(Länge des drakonitischen Monats) z.B. 223/242, was etwa 18
Jahren enstpricht. In diesem Rhythmus wiederholen sich Sonnen- und
Mondfinsternisse.

Grüße
Dixon

 

Re: Über einige irreguläre Kettenbrüche
von weserus am Mi. 02. März 2011 17:37:44


Hallo Hans-Juergen,

danke für den Artikel und die interessanten Kettenbrüche.
An Deinen Artikeln gefällt mir insbesondere weiter, dass Du genau
die Quellen und Fundstellen angibst bzw. verlinkst.

freundliche Grüße Peter


Zurück zur Themenübersicht, Teil 2