Über Grenzen des menschlichen Verstandes
Die Grenzen des Verstandes sind bei einzelnen
Menschen unterschiedlich weit gesteckt. Denjenigen, die der Mathematik fern
stehen (und zum Teil sogar stolz darauf sind), fällt bereits eine der
beliebten, in Rätselzeitschriften und anderswo zu findenden Altersaufgaben wie
die folgende nicht leicht: *
Hierbei wird der Satz von Pythagoras angewendet. (Natürlich ist das Bild nur eine
grobe Veranschaulichung des Verfahrens. Rein gedanklich müsste der Kreisbogen
unendlich dünn sein; dann würde man ihn aber nicht mehr sehen.)
*
Zum Abschluss nochmals ein Problem aus dem Bereich der Logik, das weder mit dem
Unendlichen noch mit dem ominösen Punktbegriff zu tun hat und bei dem es auch
nichts zu rechnen gibt. Dieses Problem beschäftigte führende Denker bereits in
der Antike und wird auch in der Bibel erwähnt.[3] Es lautet:
Zu diesem Thema ist im Laufe der Zeit schon vieles geschrieben worden, doch
möchte ich es hier ein weiteres Mal wagen.
Verstand kommt von verstehen und bezeichnet unter anderem die
Fähigkeit, den Sinn eines Ereignisses oder einer Aufgabenstellung zu erfassen,
eine Sache zu analysieren und zutreffend zu beurteilen, richtige
Schlussfolgerungen zu ziehen usw. Er ist großenteils angeboren, kann aber durch
Erziehung und Ausbildung verstärkt und vertieft werden.
Verstand ist begrenzt. Gegen manches sträubt er sich, weil es ihm absurd erscheint.
Anderes trägt dazu bei, ihn zu verwirren. Es gibt Fragestellungen, bei denen er
machtlos ist.
Alex und Bert waren vor 7 Jahren zusammen dreimal so alt wie vor 17 Jahren, und
Bert war vor 5 Jahren viermal so alt, wie Alex vor 19 Jahren war. Wie alt sind
die beiden heute?
Gezieltes Raten und Herumprobieren kann zum richtigen Ergebnis führen;
günstiger ist die mit geringem gedanklichen Aufwand verbundene Aufstellung von
Gleichungen und deren schematische Lösung.
Auch bei (für den Kenner) einfachen Logik-Aufgaben gelangt der
Ungeübte schnell an seine Grenzen. Ein bekanntes Beispiel ist diese:
Alex sagt: "Bert lügt." Bert sagt: "Clemens lügt." Clemens
sagt: "Ihr lügt alle beide!" Was folgt hieraus, d. h. wer von den
dreien lügt nun wirklich, und wer spricht die Wahrheit?
Bei vorhandenen Grundkenntnissen in formaler Logik ist die Aufgabe leicht
lösbar, während man sich beim Versuch, mit ihr nur im Kopf, "rein
verstandesmäßig", fertig zu werden, ganz schön anstrengen muss. [1]
Bei bestimmten Dingen haben auch Mathematiker große
Schwierigkeiten. Als Beispiel diene das Folgende:
Nicht nur die ganzen Zahlen lassen sich durch Punkte auf
einer Geraden markieren, sondern auch diejenigen, die aus den ganzen
Zahlen durch Division entstehen. (Beispiel: 13/5=2,6 im Bereich zwischen den Punkten für die Zahlen 2 und 3.)
Diese Zahlen der Form p/q (p,qє Z, q≠0) und rational genannt, haben eine
besondere Eigenschaft: wenn man zwei beliebige von ihnen nimmt, a und b, und
ihr arithmetisches Mittel m1 bildet, so ist dieses ebenfalls
rational, und sein Markierungspunkt auf der Zahlengeraden liegt genau in der
Mitte zwischen a und b. Wird nun von a und m1 das Mittel m2 gebildet,
liegt dessen Punkt in der Mitte zwischen a und m1. Dies lässt sich
unendlich weiter fortsetzen (so sagt man) und führt zu der anschaulichen Vorstellung,
dass die Markierungspunkte der rationalen Zahlen überall dicht liegen.
Das heißt: in jedem noch so kleinen Intervall der Zahlengeraden gibt es
unendlich viele rationale Punkte, die unmittelbar, ohne Zwischenraum,
aneinandergrenzen. ("Rationaler Punkt" ist eine Kurzsprechweise für
"Markierungspunkt einer rationalen Zahl".)
Nun aber gibt es Zahlen, die sich nicht in der oben genannten Form
p/q darstellen lassen und die deshalb irrational genannt werden.
Für einen Teil von ihnen kann man ebenfalls Markierungspunkte auf
die Zahlengerade setzen, und zwar sehr leicht mit Zirkel und Lineal wie hier:

Dass es möglich ist, irrationale Zahlen ebenfalls auf der Zahlengerade zu
markieren, ist erstaunlich. Es kollidiert mit der Vorstellung, dass die rationalen Markierungspunkte
überall dicht liegen. Wie sollen irrationale Punkte
(von denen es unendlich viele gibt, denn die obige Figur ist nur ein
beliebig herausgegriffenes Beispiel), zwischen ihnen noch Platz finden? Hier
deutet sich ein Widerspruch an, der anscheinend darauf beruht, dass der Begriff "Punkt" nicht ausreichend genau definiert ist.
"Ein Punkt hat keine Teile", heißt es bei Euklid. Diese
Erklärung hilft im vorliegenden Zusammenhang nicht weiter; andere kenne ich
nicht. (Bei Wikipedia liest man hier: "Von Oskar Perron stammt die
Bemerkung: 'Ein Punkt ist genau das, was der intelligente, aber harmlose,
unverbildete Leser sich darunter vorstellt.' " und an anderer Stelle:
"Punkt - ein nichtausgedehnter Ort". Beides ist auch nicht gerade
erhellend.) Insgesamt bleibt ein Punkt in der Mathematik nach meinem Eindruck
etwas Geheimnsivolles, Unbestimmtes. Deshalb gehen die meisten diesem
schwierigen Begriff, der bei längerem Nachdenken den Verstand arg strapaziert,
am liebsten aus dem Weg.
Die es nicht tun, betrachten anstelle einzelner Punkte oftmals eine unendliche
Menge von ihnen, die dicht beieinander stehen und ein sogenanntes Kontinuum bilden.
(Was "dicht beieinander" bedeutet, kann und will ich hier nicht
spezifizieren.) Ein Kontinuum kann eine eindimensionale Gerade oder Strecke,
eine zweidimensionale Fläche oder ein dreidimensionaler Raum sein.
Höherdimensionale Kontinua, die sich der Anschauung entziehen, sind ebenfalls
denkbar.
Kontinuumseigenschaften zu untersuchen, ist manchmal nicht ganz ungefährlich.
Lässt man sich zu sehr und zu lange darauf ein, ohne dass greifbare und
befriedigende Erfolge eintreten, kann es einem so gehen wie Georg Cantor (1845-1918),
dem Begründer der Mengenlehre. In dem Buch [2] wird berichtet, dass er bei der
Erforschung des Kontinuums in seinen letzten Lebensjahren nicht nur schwer
depressiv wurde, sondern dabei an den Rand schwärmerisch-mystischen Wahnsinns
geriet. Der Autor des Buches ist nicht irgendein fachfremder
Wissenschaftsjournalist, sondern ein amerikanischer Mathematikprofessor, der
sich gründlich mit Cantor und der Kontinuumsforschung, auch in neuerer Zeit,
beschäftigt hat.
Auf S. 219 schreibt er:
"Zahlen gibt es, und zwar, wie ich glaube, unabhängig vom Menschen. In
einem anderen Universum - ohne Menschen und ohne irgendwelche Dinge, die wir
aus unserem Universum kennen - gäbe es trotzdem Zahlen, die unendlich wären.
Doch wie dicht wären diese Zahlen? Gibt es das Kontinuum tatsächlich? Ist es
möglich, dass zwar die Zahlen existieren, aber das Kontinuum nicht? …"
Unendlich (auch "unendlich benachbart"), Punkt, Kontinuum -
dies sind Begriffe und Untersuchungsgegenstände meist hochkarätiger
Mathematiker und Spezialisten auf den betreffenden Gebieten. Kehren wir deshalb
zu denen zurück, die sich, sei es aus beruflichem Interesse, sei es aus
Liebhaberei, mit einfacheren Matheproblemen beschäftigen. Ihnen wird, zum Teil
schon in der Schule, beispielsweise eine solche Aufgabe gestellt:
Angenommen, die Erde sei eine ideale Kugel ohne Berge und Täler. Um ihren
äquator wird ein Faden, der einen Meter länger als der Erdumfang ist, gelegt
und zwar so, dass der Abstand zwischen ihm und der Erdoberfläche überall gleich
groß bleibt. Kann nun, so lautet die Frage, unter dem Faden noch ein kleines
Tier hindurchschlüpfen, z. B. eine Ameise, eine Laus oder vielleicht gar nur
eine "Bazille" ?
Bei dieser Aufgabe spielt das Unendliche keine Rolle; wir bleiben ganz im
Endlichen. Trotzdem ist es dem untrainierten Verstand nicht ohne Weiteres
möglich, bei der ungeheuren Größe des Erdumfangs die Wirkung von dessen
Verlängerung um einen Meter richtig einzuschätzen. Man neigt leicht dazu, den
Abstand des Fadens von der Erdoberfläche als sehr klein anzusehen. Die Rechnung
ist einfach und ihr Ergebnis verblüffend: unter dem Faden kann sich sogar ein
Eichhörnchen oder eine kleine Katze mühelos hindurchbewegen! (Dieses
unerwartete Resultat lässt sich besser verstehen, wenn die Erde durch sehr viel
kleinere runde Gegenstände wie Schüsseln, Trinkgläser oder Münzen ersetzt wird
und man damit und einem Faden praktische Versuche anstellt.)
Eine andere Aufgabe, die mir kürzlich ein Bekannter stellte, lautet:
Um die Erde wird unter derselben Voraussetzung wie oben ebenfalls ein Faden
gelegt, der um 1m länger als der Erdumfang ist. Dieser wird aber jetzt an einer
Stelle hochgezogen, so dass er mit seinem restlichen Teil eng an der Erde
anliegt. Die nicht maßstäbliche Figur zeigt, was gemeint ist:
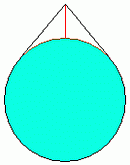
Die rote Strecke kann man sich als einen Stock denken, und die Frage lautet,
wie lang dieser wohl sein muss: vielleicht auch nur ein paar Zentimeter wie bei
der ersten Aufgabe?
Auch hier versagt bei den meisten die innere Vorstellung, und man muss rechnen,
um Genaueres zu erfahren.
"Ein Kreter sagt: alle Kreter lügen immer",
und die Frage ist, was man von dieser Aussage zu halten hat.
Ist sie wahr, muss sie zugleich falsch sein, denn sie stammt von einem Kreter, der, wie sie behauptet, immer lügt.
Das ist verwirrend und zeigt ebenfalls eine Grenze des menschlichen Verstandes auf.
[1] (Nicht auf dem Matheplaneten.) Wer an den Lösungen der beiden Aufgaben interessiert ist, klicke hier.
[2] Amir D. Aczel: Die Natur der Unendlichkeit, rororo, ISBN 3 499 61358 1
[3] Titus1,12
4.10.06
Nachtrag 2023: Was KI zum Kreter-Problem meint
Zurück zur Themenübersicht, Teil 2