Kürzlich war ich in Basel, der Geburtßtadt Leonhard Eulers (1707-1783). Auf der Rückfahrt kam mir der Gedanke, etwas über die nach ihm benannte Zahl e zu schreiben, die in vielen Bereichen der Wissenschaften anzutrefffen ist. Das meiste des Folgenden wird auf dem Matheplaneten Studenten, fertig ausgebildeten Mathematikern und Physikern sowie Lehrern, aber auch Ingenieuren verschiedener Gebiete bekannt sein; so wende ich mich hauptsächlich an Schüler.
Als Eulersche Zahl bezeichnet man den Grenzwert
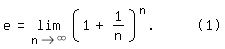
Entstanden ist (1) im Zusammenhang mit überlegungen zur Zinseszinsrechnung, die auch Unterrichtsgegenstand in der Schule ist. Ausführlich wird darüber zum Beispiel hier [1] berichtet.
e angenähert nach der obigen Definition zu berechnen, ist mühselig. Wohl niemand hat große Lust, etwa für n=10 die Zahl 1+1/10=1,1 zehnmal mit sich selbst zu multiplizieren. Das ginge noch an, erhielte man dabei einen einigermaßen genauen Näherungswert für e, doch ist das nicht der Fall. Selbst bei n=100,1000,10000 ist man noch weit von dem Wert entfernt, der vom Taschenrechner mit 2,718281828 angegeben wird. Er sieht aus wie der Anfang eines periodischen Dezimalbruchs, doch ist e in Wirklichkeit eine transzendente Zahl mit unendlich vielen, unregelmäßig aufeinander folgenden Ziffern.
Natürlich hatte Euler vor über 250 Jahren nicht unser modernes Rechenhilfsmittel zur Verfügung, aber auch stures, sehr häufiges Multiplizieren derselben Zahl mit sich selbst kam für ihn nicht in Frage.
Wie er "seine" Zahl, zunächst noch mit a bezeichnet, auf 23 Nachkommastellen genau berechnete, kann man hier [2] nachlesen. Die Herleitung ist nicht für jeden einfach zu verstehen, ganz abgesehen davon, dass der Text in lateinischer Sprache geschrieben wurde; auch in der deutschen übersetzung [3] fällt das nicht gerade leicht.
Ich folge deshalb nicht dem Vorbild Eulers, sondern wende den Binomischen Lehrsatz an. In einfacher Form lautet er:
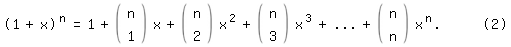
Die Klammerausdrücke heißen Binomialkoeffizienten und sind die Zahlen des Pascalschen Dreiecks1), das schon chinesischen Mathematikern des 13. Jahrhunderts bekannt war:
1) Zur Kontrolle rechne man nach:
(1+x)1=1+1x; (1+x)2=1+2x+1x2; (1+x)3=1+3x+3x2+1x3; (1+x)4=1+4x+6x2+4x3+1x4 usw.
Das Bildungsgesetz für die Binomialkoeffizienten ist leicht zu erkennen. Um aber einen bestimmten, im Pascalschen Dreieck weiter unten liegenden Binomialkoeffizienten zu erhalten, muss man, wenn dieses benutzt werden soll, die vorhergehenden berechnen. Ohne Dreieck ist das nicht nötig, denn mit der Abkürzung n! (gespr. "n-Fakultät") für das Produkt 1⋅2⋅3⋅...⋅n gilt auch noch
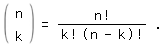
(Begründung s. [4], Abschnitt "Der Binomialkoeffizient in der Kombinatorik".)
Speziell ergibt sich
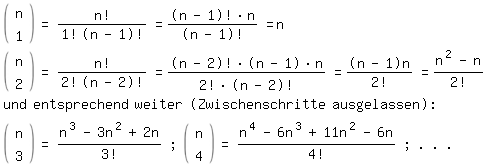
Ersetzen wir nun in (2) x durch 1/n, entsteht:
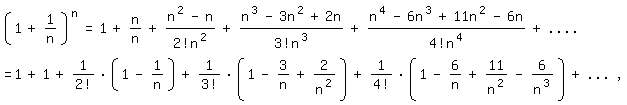
und wenn man hierin n gegen Unendlich gehen lässt, bleibt ein anderer, wohlbekannter Ausdruck für die Euler-Zahl übrig:
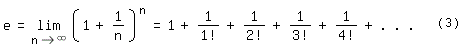
Diese Art der Darstellung von e mit einfachen Divisionen und Additionen sowie durch die rasch ansteigenden Fakultäten eignet sich gut für die angenäherte numerische Berechnung. Geht man bis zum Glied mit 12!, ergibt sich der oben genannte, vom Taschenrechner angezeigte Näherungswert.
Bei den Anwendungen ist die Zahl e nicht nur für sich allein von Interesse, sondern vor allem als Basis einer Potenz. Die Funktion mit der Gleichung f(x) = ex heißt Exponential- oder einfach nur e-Funktion. Für sie ergibt sich, ausgehend von
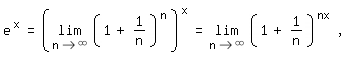
und ebenfalls mit Hilfe des Binomischen Lehrsatzes die unendliche Reihendarstellung
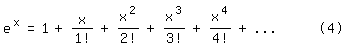
Leitet man dies nach x ab, entsteht
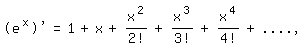
d. h. wieder die e-Funktion!
Es ist nicht nur (ex)'=ex, sondern (nach der Kettenregel der Differentialrechnung) auch (ekx)'=k⋅ekx sowie (A⋅ekx)'=A⋅k⋅ekx, wobei k und A Konstanten sind. Falls also gilt:
f(x)=A⋅ekx, gilt auch f'(x)=k⋅f(x).
Diese Gleichung wird Eulersche Relation genannt. Unter anderem bildet sie die Grundlage großer Teile der Wechselstromtechnik. Dort redet man viel von komplexen Spannungen, Stromstärken und Widerständen der Form a+bj (a,b, reell; j steht für i) und rechnet mit ihnen, obwohl es sich dabei eigentlich um reelle Größen handelt. Diese scheinbare Umständlichkeit ist praktisch: durch sie wird der Schreibaufwand gegenüber Rechnungen ganz im Reellen erheblich verringert, und es lassen sich Eigenschaften von Wechselstromschaltungen durch Zeigerdiagramme veranschaulichen.
In der Mechanik wird die Form einer lose durchhängenden Kette (eines Seils, einer Hochspannungsleitung)
Die Eulersche Zahl und Relation sind nicht die einzigen mathematisch-physikalischen Objekte, die mit dem Namen des großen Schweizer Gelehrten verbunden sind. Viele seiner weiteren Entdeckungen und Neuschöpfungen sind in [7] aufgeführt.
Dies findet eine Anwendung bei Wachstumsprozessen. Bei ihnen bedeutet die Variable x
die Zeit t, und man setzt traditionell nach Newton über das Funktionszeichen einen Punkt anstelle des sonst angehängten Strichs. Bedeutet etwa G(t) die aktuelle Gesamtzahl der Bakterien einer Kultur, dann bezeichnet Ġ(t) die Geschwindigkeit, mit der sie zunimmt.
Beobachtet wird oft eine Proportionalität zwischen beiden, und aus Ġ=k⋅G schließt man nach Obigem, dass bei positivem k die Anzahl der Bakterien exponentiell mit der Zeit zunimmt: G=Goekt. Dabei ist Go die Bakterienanzahl zur Zeit t=0. (Probe: Ġ = (Goekt). = Gokekt
= kGoekt = kG, wie vorausgesetzt.)
Ist k negativ, nimmt die Population mit der Zeit exponentiell ab. Dies geschieht beim radioaktiven Zerfall.
Schaltet man eine Gleichspannungsquelle Uo mit einem Widerstand R und ursprünglich ungeladenem Kondensator C in Reihe, so nimmt die Stromstärke nach dem Schließen des Schalters ebenfalls exponentiell ab, I=(Uo/R)⋅e-t/RC, während die Kondensatorspannung gemäß UC=Uo(1-e-t/RC) zunimmt.
Wird anstelle einer Gleich- eine Wechselspannungsquelle verwendet, kommt eine weitere Eigenschaft der e-Funktion zum Tragen.
Schon lange vor Euler war es üblich, gewisse irrationale und transzendente Funktionen durch Reihen mit einfachen rationalen Gliedern anzunähern. Dazu diente unter anderem die Reihe von McLaurin (1698-1746):
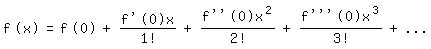
Mit ihr ergeben sich die Reihen für Sinus und Kosinus:
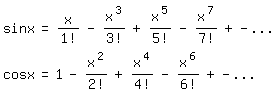
Ersetzt man in (4) x durch ix, wobei i die imaginäre Einheit mit i2=-1 bedeutet, entsteht die Reihe
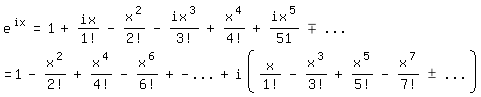
d. h, es ist
eix = cos x + i sin x. (5) 2)
Ein Sonderfall von (5) für x=π ist die Gleichung
eiπ + 1 = 0 ;
sie wird von manchen als die schönste Formel in der Mathematik angesehen.3) Weiter kann man mit (5) auch berechnen, was
z. B. ii ist (mit dem wohl erstaunlichen Resultat, dass dabei etwas Reelles herauskommt).
im wesentlichen durch die Gleichung y = ex + e-x beschrieben, vgl.
z. B. [5], und beim Anlegen von Schiffen im Hafen spielt die e-Funktion ebenfalls eine Rolle. Mit einem um einen Poller geschlungenen Seil (evtl. mehrfach) kann man selbst ein großes Schiff von Hand zum Halten bringen.[6]
Leonhard Euler war bis an sein Lebensende, inzwischen gänzlich erblindet, von nicht nachlassender, bewundernswerter Kreativität. Gerühmt werden seine menschlichen Eigenschaften: er war geduldig, großzügig, hilfsbereit, humorvoll. Und bescheiden: auf seine Entdeckungen bildete er sich nichts ein und war, anders als einige seiner Berufskollegen, nie in Prioritätsstreitigkeiten verwickelt. Euler glaubte an Gott und war ein frommer Christ.[8] Einen sehr informativen Artikel über ihn findet man im Internet bei [9] und eine Biographie Eulers in [10].
(Basel, Nähe Bahnhof)
2) In seinen Lectures on Physics, Abschnitt 22-6, bezeichnete der amerikanische Physiker und Nobelpreisträger Richard Feynman die Gl. (5) als "unser Juwel", ohne ihren Entdecker Euler zu erwähnen. Die Herleitung geschieht umständlich numerisch und mit etwas Herumprobieren (" After a little trial and error, we discover ...").
3) Dazu gibt es diesen hübschen Limerick, mehrfach im Internet:
"I used to think math was no fun,
'Cause I couldn't see how it was done.
Now Euler's my hero,
For I now see why 0
Equals e to the i pi plus 1."
(Anm.: "e to the i pi" bedeutet: "e hoch i pi", und "0" wird wie "zero" ausgesprochen.)
[1] http://www.poenitz-net.de/Mathematik/5.Analysis/5.7.8.S.Euler.pdf
[2] Introductio in Analysin Infinitorum, Band 1, S. 90
[3] deutsche übersetzung der "Introductio" (Dort steht der erwähnte, 23-stellige Näherungswert für die Euler-Zahl auf S. 91.)
[4] http://de.wikipedia.org/wiki/Binomialkoeffizient
[5] http://matheplanet.com/matheplanet/nuke/html/article.php?sid=506
[6] http://de.wikipedia.org/wiki/Euler-Eytelwein-Formel "Einmal um den Poller wickeln!"
[7] https://de.wikipedia.org/wiki/Wißenschaftliches_Werk_Leonhard_Eulers
[8] "Ein großer Gelehrter und ein gütiger Mensch" (Ergänzung: in Berlin, wo er 25 Jahre lang wirkte, gehörte Euler zum Konsistorium der französisch-reformierten Kirche.)
[9] "Leonhard Euler und die Wonnen der Wissenschaft"
[10] "https://web.archive.org/web/20100227064158/http://www.et.fh-koeln.de/ia/ma/euler.html"
Die Eulersche Relation (5) wird in Lehrbüchern und im Internet gewöhnlich wie oben mit Hilfe unendlicher Reihen hergeleitet, doch ist dieser Beweis nicht naheliegend. Auch sind die dabei verwendeten drei Reihen nicht jedem geläufig und werden unbewiesen nur zitiert. Ohne sie kann man so vorgehen: eix ist eine komplexe Zahl a + i b. Darin bedeuten a und b keine festen Zahlen, sondern Funktionen von x. Es soll also sein:
eix = a(x) + i b(x). Dann folgt: (eix)' = i eix= a'(x) + i b'(x), (eix)" = -eix = a"(x) + i b"(x), eix = -a"(x) - i b"(x). Wegen eix = a(x) + i b(x) ist
a"(x)=-a(x) und b"(x)=-b(x) mit den Lösungen a(x) = sin x oder a(x) = cos x sowie b(x) = sin x oder b(x) = cos x.
Wir haben also theoretisch vier Möglichkeiten zur Darstellung von eix durch die beiden Winkelfunktionen Sinus und Kosinus: es ist entweder
eix = sin x + i sin x oder eix = cos x + i cos x oder eix = sin x + i cos x oder eix = cos x + i sin x . Nur die letzte kommt in Frage, denn für x=0 muß sich auf beiden Seiten des Gleichheitszeichens 1 ergeben; somit ist eix = cos x + i sin x , was zu zeigen war.
Umgekehrt: sei f(x) = cos x + i sin x, dann gilt: f '(x) = - sin x + i cos x = i(cos x + i sin x) = i f(x), also f '(x)/f(x) = i. Integration ergibt:
ln f(x) = ix + C, f(x) = eix+ C = eCeix. Da f(x) für x=0 gleich 1 ist, muß C= 0 sein; d. h. es ist f(x) = cos x + i sin x = eix. Auch diese einfache Herleitung der Eulerschen Relation sah ich noch nirgends.
Zurück zur Themenübersicht