Vorbemerkung: Mehrere in letzter Zeit auf dem Matheplaneten erschienene Artikel erfordern sehr spezielle Kenntnisse und sind dadurch vermutlich nur relativ wenigen verständlich. So ist es vielleicht ganz angenehm, zur Abwechslung wieder etwas Einfacheres zu lesen.
Mein Thema sind zunächst nochmals die Hüllkurven, Einhüllenden oder Enveloppen, die auch schon in [1] und [2] behandelt wurden; darauf werde ich gelegentlich zurückgreifen.
Bei fast allen der bisher betrachteten Beispiele bestanden die Scharen, zu denen die Hüllkurve gesucht wurde, aus geschlossenen Kurven (Ellipsen, Kreisen und anderen); nur beim letzten Beispiel von [1] handelte es sich um eine Geradenschar.
Mit einer solchen möchte ich hier fortfahren.
Die Schargeraden sollen die Achsen so schneiden, daß die Summe der Achsenabschnitte xo und yo konstant bleibt, xo+yo=c, wobei das Vorzeichen zu berücksichtigen ist. So gehören, wenn z. B. c=5 ist, die beiden Geraden g1 mit xo=2, yo=3 und g2 mit xo=7, yo=-2 zu der Schar. Nimmt man mehr von ihr hinzu, entsteht dieses Bild:

Die rote Kurve sieht aus wie eine Parabel. Daß sie tatsächlich eine ist, soll jetzt gezeigt werden.
Als nächstes betrachte ich eine Geradenschar, bei der das Produkt der Achsenabschnitte konstant ist: xoyo=c2.
Analog zum Vorgehen bei der Parabel ergibt sich für die Einhüllende y=c2/(4x), d. h. die Gleichung einer Hyperbel mit folgendem Bild:
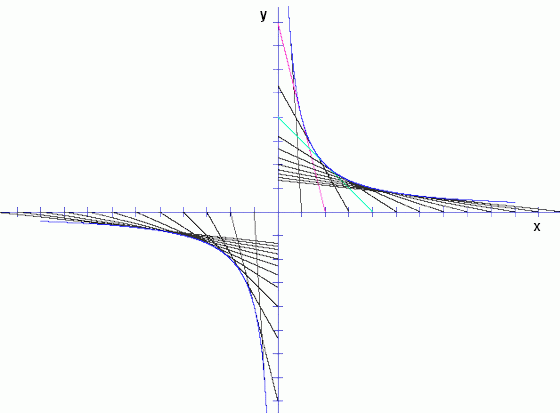
Kontrollieren kann man an der grünen und roten Gerade, daß in diesem Fall xoyo=16 ist, die gezeichnete Hyperbel also die Gleichung y=4/x hat.
Bei der Geradenschar mit der etwas komplizierteren Beziehung b2xo2+ a2yo2= xo2 yo2 zwischen den beiden Achsenabschnitten (a, b konstant) ergibt sich nach demselben Schema die Gleichung einer Ellipse mit den Halbachsen a und b:
.png)
.png)
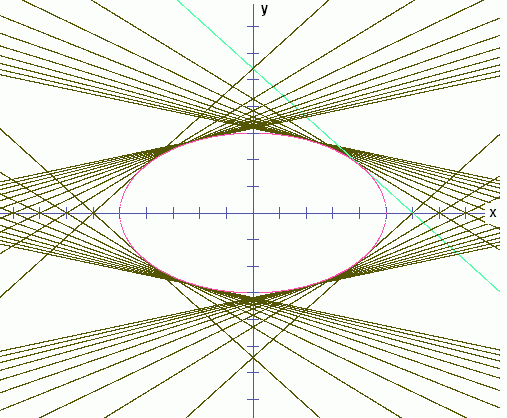
Die grüne Gerade erfüllt die Auswahlbedingung für die beiden Achsenabschnitte in der Form b2/yo2+a2/xo2=1. Wir lesen ab xo=6 und schätzen yo=5,4. Dann ist mit a=5, b=3:
.png)
wie es (angenähert) sein soll.
Wenn man eine bestimmte Kurve zusammen mit den sie einhüllenden Geraden haben möchte, ist es, von Ausnahmen abgesehen, sehr schwierig bis unmöglich, sich eine Beziehung zwischen ihnen auszudenken, die genau die gewünschte Kurve ergibt. Viel einfacher ist es dagegen, man beginnt mit dieser und bestimmt die Schar ihrer Tangenten. Liegt die Gleichung der Hüllkurve in kartesischen Koordinaten und in expliziter Form y=f(x) vor, und ist P(xp,yp) ein Punkt, in dem eine beliebige Gerade der Schar die Kurve berührt; ist außerdem X(x,y) ein anderer Punkt auf dieser Tangente, dann gilt
.png)
wobei f '(xp) die Ableitung der Hüllkurve an der Stelle xp bedeutet.
Hieraus ergibt sich
y = f '(xp) x - f '(xp) xp + f(xp) ,
und das ist die gesuchte Gleichung der einhüllenden Geradenschar mit xp als Parameter.
Dies können wir bei der "Versiera" oder "Locke der Agnesi" [3] mit der Gleichung y=a/(1+x2) anwenden:
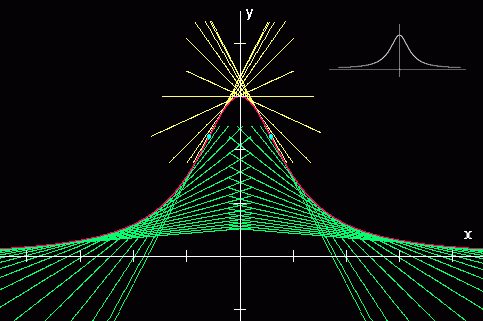
Die Tangenten verlaufen wegen der beiden Wendepunkte oberhalb und unterhalb der Kurve. Ihre Gleichung lautet:
.png)
Bei der folgenden dekorativen Figur ist im unteren Bereich die Kurve mit der Spitze nicht die Hüllkurve von Geraden, sondern von gleich langen Strecken. Sie enden auf einer weiteren Kurve, die Ähnlichkeit mit einer Ellipse hat:
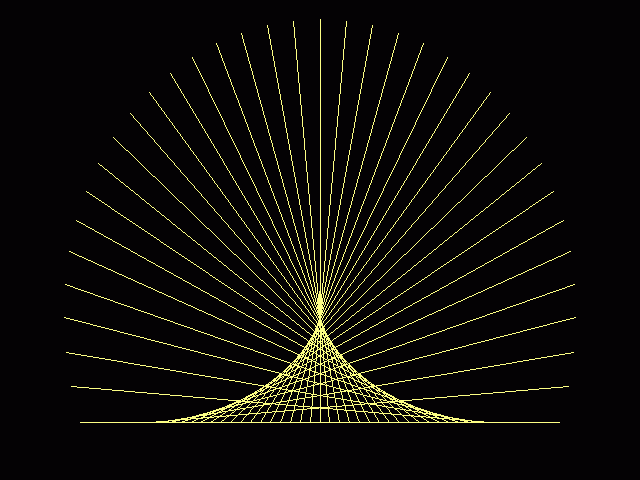
Abschließend eine Figur, die ebenfalls aus lauter Strecken besteht und einen eigentümlich-räumlichen Eindruck vermittelt: [4]
.png)
[1] Über Hüllkurven
[2] Die Kardioide als Hüllkurve
[3] Kurvenverwandtschaft bei w=1/z Fig. 5 u. 2 Disk.beiträge v. 21.6.
[4] fedgeo Parameterkurven Beitrag Nr. 49 von Matroid
Re: Über Kurven und Figuren, die von Geraden und Strecken erzeugt werden |
Netter, kleiner Artikel! Viele Grüße Florian |
Re: Über Kurven und Figuren, die von Geraden und Strecken erzeugt werden |
Endlich mal wieder ein Artikel, den ich lesen wollte. |
Re: Über Kurven und Figuren, die von Geraden und Strecken er |
Interessant und vor allem einfach zu verstehen =) gefällt mir. Zurück zur Themenübersicht, Teil 2 |